→ 이 글은 「이득우의 게임 수학」을 바탕으로 작성했습니다.
■ 벡터의 내적(Dot Product)
내적은 같은 차원의 두 벡터가 주어졌을 때 구성하는 성분을 곱한 후 더해 "스칼라"로 만든다.
$$ \vec u \cdot \vec v = x_1\cdot x_2 + y_1\cdot y_2 $$
▼ 내적의 성질
| 곱셈과 덧셈으로 구성되어 있어 교환법칙이 성립한다. | $\vec u \cdot \vec v = \vec v \cdot \vec u$ |
| 결과가 스칼라이기 때문에 결합법칙은 성립하지 않는다. | $\vec w \cdot (\vec u \cdot \vec v) \neq (\vec w \cdot \vec u) \cdot \vec v$ |
| 덧셈에 대한 분배법칙이 성립한다. | $\vec w \cdot (\vec u + \vec v) = \vec w \cdot \vec u + \vec w \cdot \vec v$ |
| 자기 자신을 내적한 결과는 크기를 제곱한 결과가 나온다. | $\vec v \cdot \vec v = (x^2 + y^2)$ |
| 두 벡터의 합의 내적은, 두 벡터의 크기의 합이다. | $(\vec v + \vec u) \cdot (\vec v + \vec u) = |\vec v|^2 + |\vec u|^2 + 2(\vec v \cdot \vec u)$ |
1. 내적과 삼각함수
두 백터의 사잇각을 $\theta$라 한다면, 내적과 $\cos$함수의 관계는 다음과 같다.
$$ \vec v\cdot \vec u = |\vec v||\vec u| \cos \theta $$
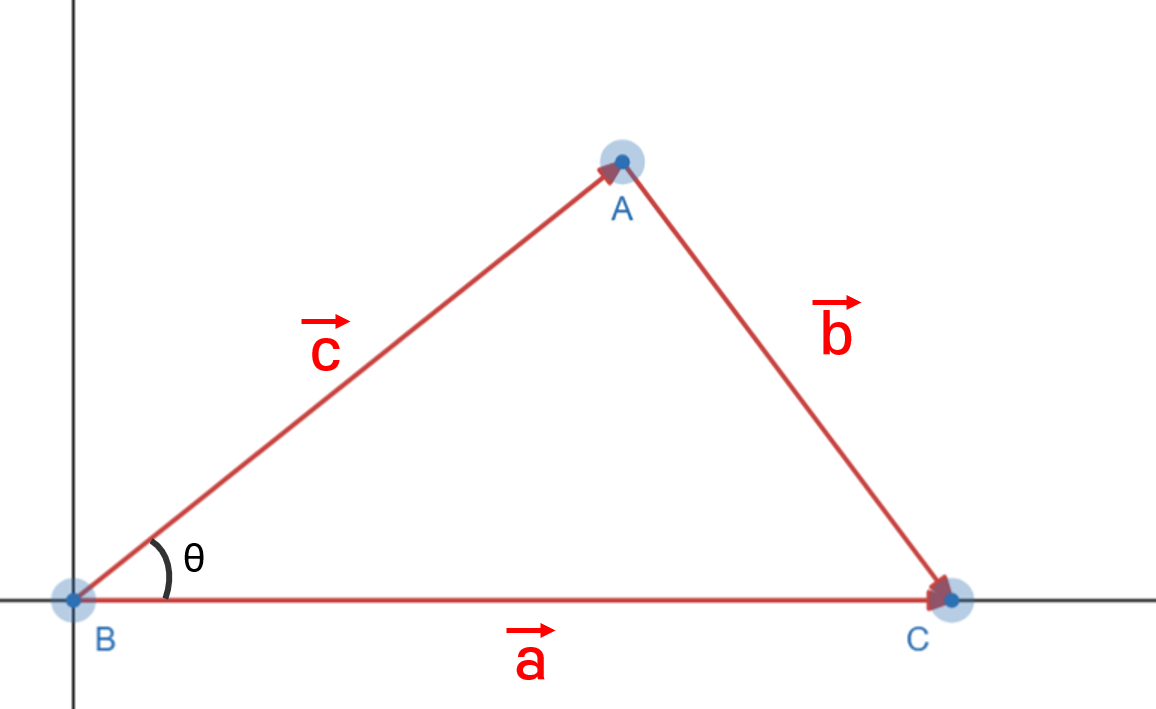
위 수식을 유도하기 위해 데카르트 좌표계에 세 점$(A,B,C)$으로 구성된 삼각형을 생성하고, 각 점을 마주 보는 벡터$(\vec a, \vec b, \vec c)$와 원점에 위치한 사잇각$(\theta)$로 구성하자.
그럼, 앞서 배운 삼각함수의 성질을 사용해 각 점의 좌표와 벡터는 다음과 같이 구할 수 있다.
| 삼각형 점의 좌표 | 변을 구성하는 벡터 |
| $A = (|\vec c| \cos \theta, |\vec c|\sin \theta)$ | 밑변 : $\vec a = C - B = (|\vec a| - 0, 0) = (|\vec a|, 0)$ |
| $B = (0,0)$ | 높이 : $\vec b = C - A = (|\vec a| - |\vec c| \cos \theta, |\vec c|\sin\theta)$ |
| $C = (|\vec a|, 0)$ | 빗변 : $\vec c = A - B = (|\vec c|\cos\theta, |\vec c|\sin\theta)$ |
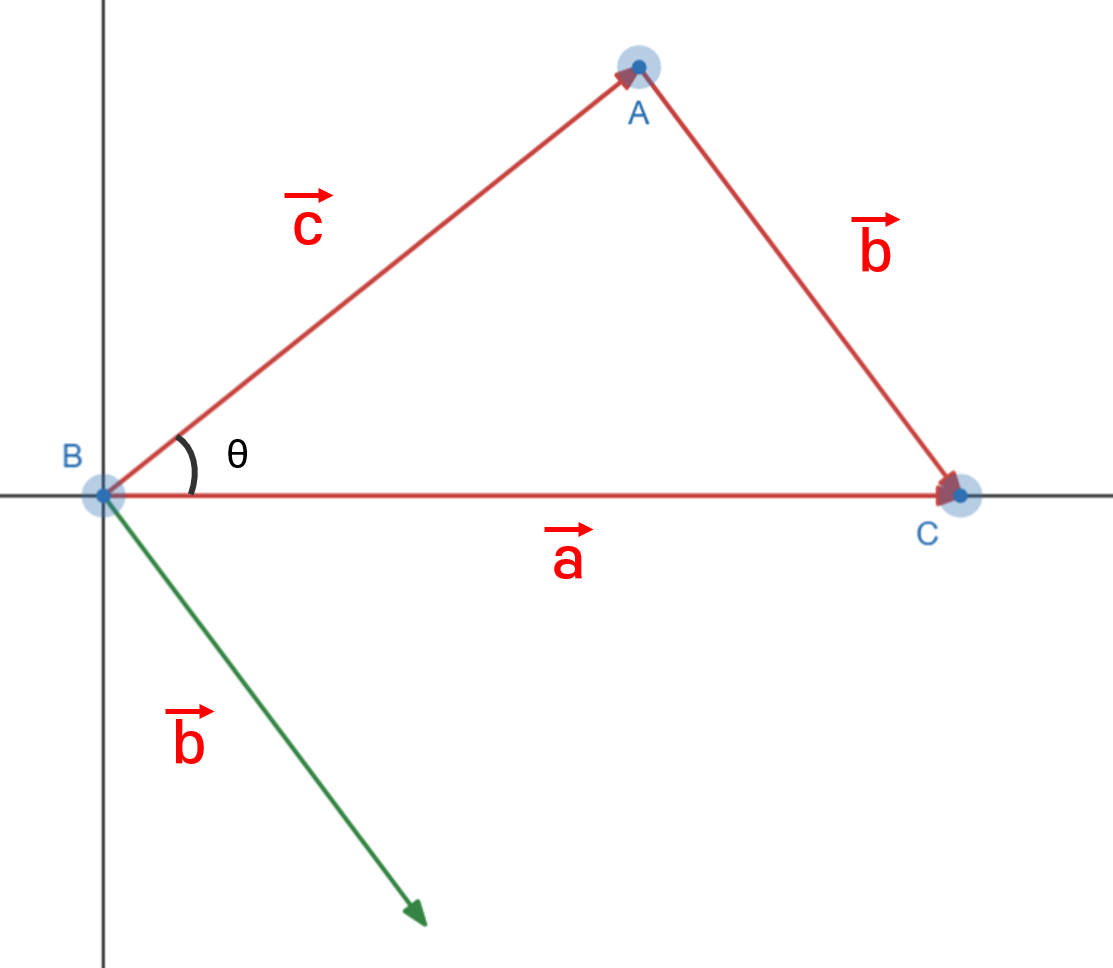
$$ \vec b = C - A = \vec a + (-\vec c) $$
여기서, 벡터 $\vec b$는 점 $C-A$로 구한 벡터이다. 점 $C$의 위치벡터가 $\vec a$. 점 $A$의 위치벡터가 $\vec c$이므로, 위와 같이 표현할 수 있다.
- 벡터의 정의상 출발점이 같은지 여부가 아니라, 좌표평면 어딘가에 그려졌더라도 “방향과 크기”만 같다면 같은 벡터로 취급한다.
이제 벡터$\vec b$의 크기를 제곱해보자. 벡터 $\vec b = (|\vec a|-|\vec c| \cos \theta, |\vec c|\sin\theta)$ 이므로, 벡터 $\vec b$를 제곱하게 되면
$$ |\vec b|^2 = (|\vec a| - |\vec c| \cos \theta)^2 + |\vec c|^2 \sin^2\theta \\ = |\vec a|^2 -2|\vec a||\vec c|\cos \theta + |\vec c|^2\cos^2\theta + |\vec c|^2 \sin^2\theta $$
위 식에서 $|\vec c|^2\cos^2\theta + |\vec c|^2 \sin^2\theta$ 이 부분은 아래와 같이 정리된다.
$$ |\vec c|^2\cos^2\theta + |\vec c|^2 \sin^2\theta \\ = |\vec c|^2(\cos ^2 \theta + \sin ^2 \theta) $$
여기서 삼각함수 항등식에 의해 $(\cos ^2 \theta + \sin ^2 \theta) = 1$이 되므로 최종적으로 식은 아래와 같이 정리된다.
$$ |\vec b|^2 = |\vec a|^2 + |\vec c|^2 - 2|\vec a||\vec c|\cos\theta $$
[벡터 크기의 제곱을 활용한 식(1)]
이번엔 같은 벡터를 내적하면 벡터 크기의 제곱이 되는 성질을 활용하여 식을 전개해 보자.
$$ |\vec b|^2 = \vec b \cdot \vec b \\ =(\vec a + (-\vec c))\cdot (\vec a + (-\vec c)) \\ = |a|^2 + |\vec c|^2 - 2\vec a\cdot \vec c $$
[자기 자신과 내적(2)]
그렇다면 식 1의 $- 2|\vec a||\vec c|\cos\theta$ 부분과, 식 2의 $-2\vec a\cdot \vec c$ 부분은 동일한 값이므로 아래의 식이 성립한다.
$$ \vec a \cdot \vec c = |\vec a||\vec c|\cos\theta $$
만약 두 벡터의 크기가 모두 1이라면, 두 벡터의 내적은 결국 cos 함수가 된다.
$$ \vec v\cdot \vec u = \cos \theta $$

두 단위벡터를 내적 했을 때, 그 값이 0이 되는 조건은 cos함숫값이 90 혹은 270(-90)이다. 따라서, 두 단위벡터의 내적값이 0이라면 두 벡터는 "직교한다".
- 또한 두 표준기저벡터가 각 세타만큼 회전한 결과$(\cos \theta, \sin \theta),\ (-\sin\theta, \cos \theta)$의 내적도 언제나 0이 나온다.
2. 행렬 곱으로 내적을 표현
$$ \begin{bmatrix} a & b \\ c& d\end{bmatrix}\begin{bmatrix} x \\ y\end{bmatrix} = \begin{bmatrix} ax + by \\ cx + dy\end{bmatrix} = \begin{bmatrix} (a,b) \cdot (x,y) \\ (c,d)\cdot (x,y)\end{bmatrix} $$
행렬을 구성하는 2개의 행벡터와 벡터를 구성하는 열벡터를 내적으로 위와 같이 표현이 가능하다.
$$ \begin{bmatrix} a & b \\ c& d\end{bmatrix}\begin{bmatrix} e & f \\ g& h\end{bmatrix} = \begin{bmatrix} (ae + bg) & (af +bh) \\ (ce+cg) & (df + dh)\end{bmatrix} = \begin{bmatrix} (a,b)\cdot (e,g) &(a,b)\cdot(f,h) \\ (c,d) \cdot (e,g) & (c,d) \cdot (f,h)\end{bmatrix} $$
또한, 행렬의 곱셈 역시 위와 같이 내적으로 표현이 가능하다.
▶ 직교 행렬
$$ Q = \begin{bmatrix} a & c\\ b & d\end{bmatrix} $$
열백터와 행벡터를 구성하는 모든 요소의 크기가 1이고, $(a,b)$와 $(c,d)$가 서로 직교하는 행렬을 직교 행렬(Orthogonal matrix)라 한다.
이러한 직교행렬의 특징은 직교행렬의 전치행렬$(Q^T)$는 역행렬이 된다.
따라서 $Q\cdot Q^T = I$ 즉, 직교행렬과 그 역행렬의 곱은 항등행렬이 되고 이는 내적을 통해 증명할 수 있다.
$$ \begin{bmatrix}a &c \\ b & d \end{bmatrix} \cdot \begin{bmatrix} a & b \\ c & d\end{bmatrix} = \begin{bmatrix}(a,c)\cdot(a,c) & (a,c)\cdot(b,d)\\(b,d)\cdot(a,c) & (b,d)\cdot(b,d) \end{bmatrix} = \begin{bmatrix} 1&0 \\ 0&1\end{bmatrix} $$
자기 자신을 내적한 결과는 크기를 제곱한 결과이므로 1, 서로 직교하는 두 벡터를 내적 하면 0이므로 결과적으로 언제나 항등 행렬임을 보장한다.
$$ R_\theta = \begin{bmatrix}\cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \\ R_\theta^T \cdot R_\theta = \begin{bmatrix}\cos^2\theta + \sin^2\theta &0 \\ 0 & \cos^2\theta + \sin^2\theta\end{bmatrix} = I $$
회전 변환행렬 역시 행벡터와 열벡터의 크기가 1이고 서로 직교하므로 직교행렬이다.
회전 변환과 같이 변환 후에도 물체의 형태가 그대로 유지되는 변환을 강체 변환이라고 한다. 강체 변환의 조건은 다음과 같다.
- 변화된 기저벡터의 크기는 1이다.
- 모든 기저벡터는 서로 직교한다.
- 행렬식 값이 1이다. $det(R) = \cos^2\theta + \sin^2\theta = 1$
■ 내적의 응용
1. 시야 판별
게임 제작에서 내적을 활용하여 다양한 시스템을 구축할 수 있는데, 그중 하나가 바로 목표물이 캐릭터의 앞에 있는지 뒤에 있는지 판단할 수 있다.
캐릭터의 정면(시선 방향)을 첫 번째 벡터로, 캐릭터에서 목표물을 향하는 벡터를 두 번째 벡터로 사용해 보자.
이 두 벡터를 내적 하여 사잇각을 구했을 때, 그 값이 양의 부호를 가진다면 캐릭터의 앞에, 음의 부호를 가진다면 캐릭터의 뒤에 있다고 판단할 수 있다.
public class DotProduct : MonoBehaviour
{
[SerializeField] private RotateAround target;
[SerializeField] private TextMeshProUGUI value;
private Vector3 _forward;
private Vector3 _targetDir;
private void Start()
{
_forward = transform.forward;
}
private void Update()
{
_targetDir = (target.transform.position - transform.position).normalized;
var dotProduct = Vector3.Dot(_forward, _targetDir);
if (dotProduct > 0)
{
// Do Something..
}
else
{
// Do Something..
}
}
}
내적을 통한 앞뒤 판별은 정말 쉽게 구현할 수 있다. 캐릭터에서 타겟으로 향하는 벡터를 구하고 정규화 한 뒤, 캐릭터의 정면 방향벡터와 내적값을 구한다.
그 뒤, 이 값이 양의 부호라면 캐릭터 앞 음의 부호라면 캐릭터 뒤에 있다고 판단할 수 있다.
2. 시야각 판별
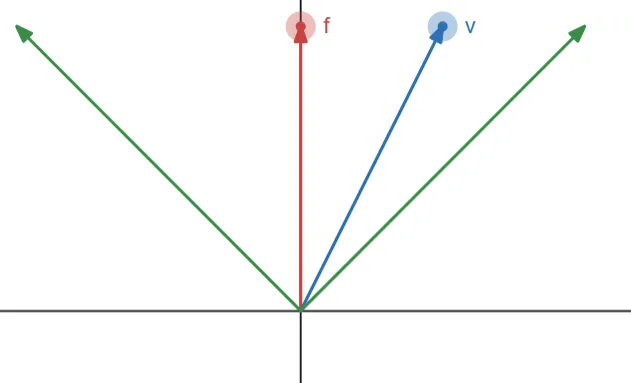
이번엔 단순 앞뒤 판별이 아닌 시야각을 지정하여 이 시야각 안에 물체가 들어왔는지 판별해 보자. 시야각 판별의 구현 순서는 다음과 같다.
- 시야각의 절반$(\frac{\theta}{2})$에 해당하는 $\cos$값을 계산한다.
- 시선 벡터와 목표로 향하는 벡터를 정규화시켜 내적값을 구한다.
- 1번의 값과 2번의 값을 비교한다.

캐릭터의 정면 벡터를 $\vec f$, 타겟까지 향하는 벡터를 $\vec t$라고 했을 때, 이 두 벡터가 단위 벡터라면 두 벡터의 내적 결과는 결국 $\vec f$와 $\vec t$가 이루는 사잇각의 $\cos$ 값(위 사진에서 d값)이 계산된다.
$\cos$함수는 각$\theta$가 커질수록 작은 값을 반환하고, 반대로 각이 작아질수록 큰 값을 반환한다.
- $\cos(0^\circ) = 1$
- $\cos(90^\circ) = 0$
- $\cos(180^\circ) = -1$
따라서, 시야각의 절반에 해당되는 $\cos$값을 $v$라 한다면,
- 내적값보다 시야각 값이 더 크다면$(d > v)$ 내적한 두 벡터가 이루는 각이 더 작음.(시야 안에 존재)
- 내적값보다 시야각 값이 더 작다면$(d < v)$ 내적한 두 벡터가 이루는 각이 더 큼.(시야 밖에 존재)
using System;
using UnityEngine;
public class FOVDetect : MonoBehaviour
{
[SerializeField] private float angle = 60f;
[SerializeField] private RotateAround target;
private Vector3 _playerForward;
private float _halfAngle;
private void Start()
{
_playerForward = transform.forward;
// 시야각 절반에 해당하는 값 미리 저장
_halfAngle = angle * 0.5f;
}
private void Update()
{
var dir = (target.transform.position - transform.position).normalized;
var dot = Vector3.Dot(_playerForward, dir);
var fov = Mathf.Cos(_halfAngle * Mathf.Deg2Rad);
DrawView();
// 시야각 안에 목표 없음
if (dot < fov)
{
target.ChangeMaterials(1);
return;
}
// 시야각 안에 목표 있음
target.ChangeMaterials(0);
}
private void DrawView()
{
var pos = transform.position;
var left = Quaternion.AngleAxis(-_halfAngle, Vector3.up) * _playerForward;
var right = Quaternion.AngleAxis(_halfAngle, Vector3.up) * _playerForward;
Debug.DrawLine(pos, pos + left * 30f, Color.red);
Debug.DrawLine(pos, pos + right * 30f, Color.red);
}
}
유니티로 구현 시, Mathf.Cos() 함수는 파라미터로 라디안 값을 받기 때문에, 기존 시야각도의 절반에 Mathf.Deg2Rad를 곱해 라디안 각도로 변환해 주면 된다.
'게임수학' 카테고리의 다른 글
| [게임수학] 6.삼각형(Mesh) (0) | 2025.09.20 |
|---|---|
| [게임수학] 6-2. 투영 벡터, Vector3.ProjectOnPlane() (0) | 2025.09.12 |
| [게임수학] 5.아핀공간 (1) | 2025.09.08 |
| [게임수학] 4. 행렬 (1) | 2025.09.05 |
| [게임수학] 3. 삼각함수 (2) | 2025.08.31 |