■ 재귀호출(Recursive call)
재귀 호출이란, 아래와 같이 함수 내에서 자기 자신을 다시 호출하는 것을 의미한다. 이렇게 함수 정의 내에서 자기 자신을 호출하는 코드가 들어있는 함수를 “재귀 함수(Recursive Function)”라 한다.
using System;
public class RecursiveTest
{
public void Recursive()
{
Console.WriteLine("Recursive Call!");
// 자기 자신 호출
Recursive();
}
}
[재귀 함수]
완료되지 않은 함수를 다시 호출한다는 것이 불가능해 보이지만, 사실 가능하다. 재귀 호출의 실행 흐름을 살펴보면 아래와 같다.
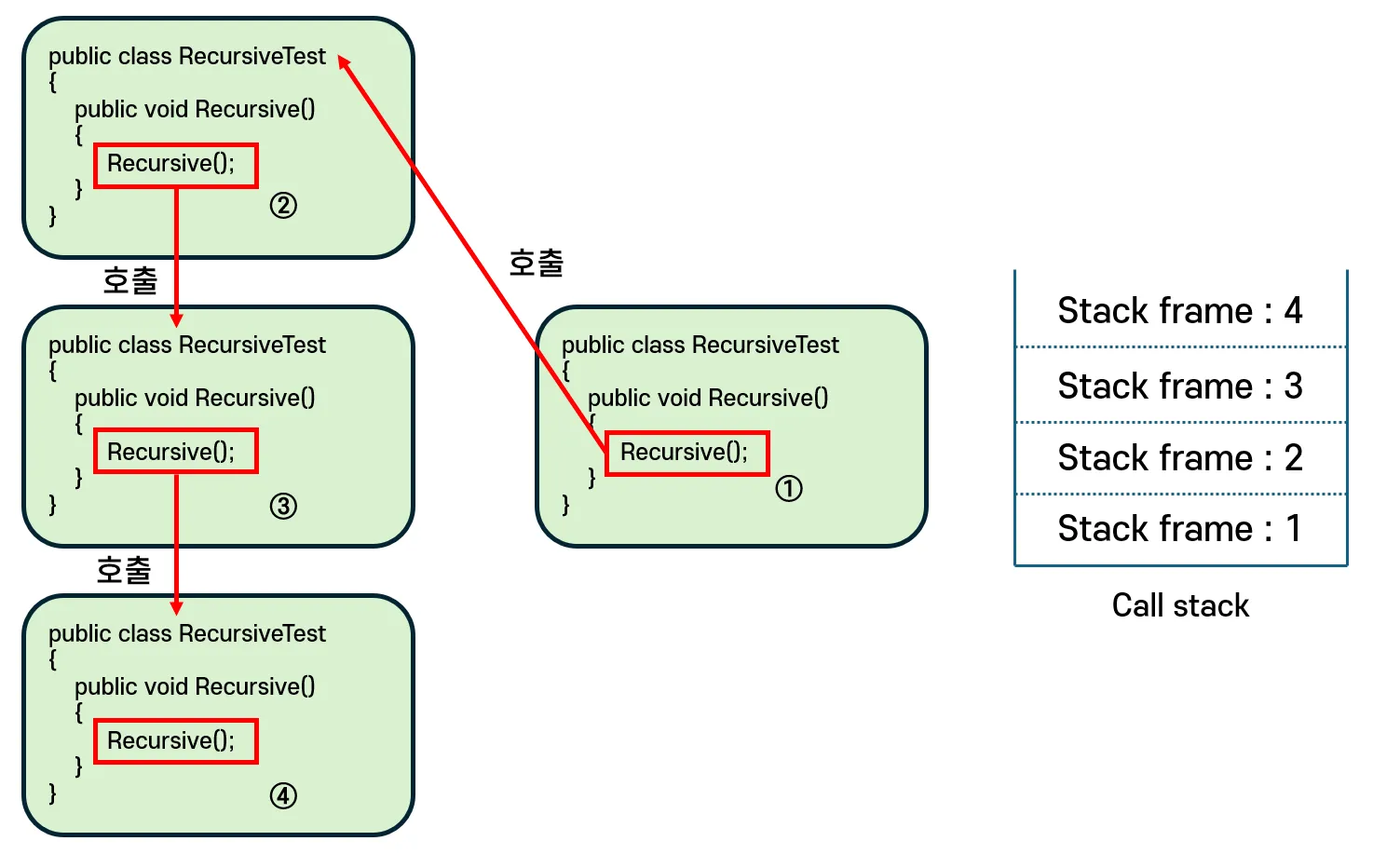
함수 내에서 자기 자신을 호출하면 프로그램 실행 흐름은 다시 함수의 시작 부분으로 이동한다.
이때 단순히 처음부터 다시 실행하는 것이 아니라, 현재 함수의 실행 상태(어디서 호출했는지, 어떤 매개변수를 받았는지, 반환값은 어디로 돌려줘야 하는지)를 “호출 스택"에 기록한다.
이 덕분에 재귀 호출이 끝나면 프로그램은 저장된 정보를 바탕으로 원래 실행하던 위치로 되돌아갈 수 있다.

앞서 작성한 재귀 함수는 한번 호출되면 탈출 조건이 없기 때문에 프로그램이 종료될 때까지 계속 호출된다.
따라서 재귀 함수를 작성할 때는 항상 함수의 “탈출 조건”을 적어줘야 한다.
using System;
public class RecursiveTest
{
public void Recursive(int num)
{
// 재귀 함수의 탈출 조건
if (num <= 0) return;
Console.WriteLine($"Recursive Call : {num}");
Recursive(num - 1);
}
}
[재귀 함수의 탈출 조건]
위 코드에선 파라미터의 값이 0 이하인 경우 함수가 종료되도록 정의하였다. 따라서 위 코드의 실행 흐름은 다음과 같이 실행된다.

재귀적으로 호출이 이뤄지는 Recursive 함수에 0이 전달되면서 “재귀의 탈출 조건”이 성립되어 함수가 반환되기 시작한다.
호출 스택에 쌓여있는 스택 프레임이 하나씩 제거되며, 실행 흐름은 이전에 해당 함수를 호출했던 위치로 돌아간다.
■ 재귀 호출의 활용
1. 팩토리얼
재귀함수는 자료구조나 알고리즘의 어려운 문제를 단순화하는 데 사용될 수 있다. 무엇보다 재귀적인 수학식을 그대로 코드에 옮길 수 있는데 대표적인 예시가 바로 팩토리얼(factorial)이다.
- 팩토리얼 값을 반환하는 함수를 재귀적으로 구현해보자.
$$ n! = n * (n-1) (n-2) * ... * 1 $$
정수 $n$팩토리얼은 $n\times(n-1)$로 표현할 수 있고, 이걸 함수 $f(n)$으로 표현하면 아래와 같이 표현할 수 있다.
$$ f(n) = \begin{cases} n\times f(n-1) & \ \ ...n \ge1 \\ 1 & \ \ ...n =0 \end{cases} $$
재귀 호출을 작성할 때의 팁은 항상 “탈출 조건”부터 만드는 것이다. 팩토리얼을 재귀 호출로 구현할 때 파라미터로 받는 n이 0이 되어 이를 그대로 반환해서 곱하면 결국 그 결과는 0이 되어버린다.
public class RecursiveTest
{
public int Factorial(int n)
{
if(n <= 0)
{
return 1;
}
}
}
- 따라서 n이 0보다 작거나 같다면, 1을 반환하여 재귀 호출을 종료할 수 있도록 한다.
다음으로 n이 1 이상이라면 수식 $n \times(n-1)$을 그대로 코드로 옮겨 적으면 팩토리얼 재귀 함수 호출 구현이 완료된다.
public class RecursiveTest
{
public int Factorial(int n)
{
if(n <= 0)
{
return 1;
}
return n * Factorial(n - 1);
}
}

재귀 호출의 순서는 이미 살펴보았지만, return을 통해 값이 거꾸로 반환되는 과정은 다소 헷갈릴 수 있다.
팩토리얼 함수의 반환 과정은 다음과 같다.

재귀 호출이 종료되면서, Factorial(0)은 탈출 조건에 의해 1을 반환한다.
이 반환값은 Factorial(1)의 계산식으로 돌아와 $1\times1$이 되어 다시 반환된다. 그 결과는 Factorial(2)의 계산에 사용되어 $2\times1$을 반환하고, 이 값은 다시 Factorial(3)으로 전달된다.
이와 같은 과정이 반복되어 최종적으로 Factorial(5)에서 $5\times 24 = 120$을 반환하게 된다.
함수가 호출될 때 “내가 어디서 호출됐는지”, “전달받은 파라미터 값”, “반환해야 할 값”을 호출 스택에 저장하기 때문에, 함수가 종료될 때 반환값을 가지고 이전의 위치로 돌아갈 수 있다.
2. 피보나치수열
$$ 0,\ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55... $$
피보나치수열(Fibonacci Sequence)도 재귀적인 형태를 띠는 대표적인 수열로, 위와 같이 전개가 된다.
- 앞의 두 숫자를 더해 뒤의 숫자를 만든다. ⇒ 첫 번째, 두 번째 값인 0, 1을 더해 세 번째 값 1이 결정된다.
즉, 피보나치수열의 $n$번째 값은 $n-1$번째 값 + $n-2$번째 값으로 결정된다. 피보나치수열을 재귀로 구현하기 위해 간단한 의사 코드를 작성해 보면,
int Fibonacci(int n) // 피보나치 수열의 n번쨰 값 반환
{
if 첫 번째 값을 요구하면
return 0;
if 두 번째 값을 요구하면
return 1;
세 번째 이후 값을 요구하면
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
이를 코드로 옮겨 적으면 아래와 같아지는데, 수학적 재귀의 표현이 그대로 코드로 옮겨지는 것을 확인할 수 있다.
public int Fibonacci(int n)
{
if(n <= 1)
{
return 0;
}
else if(n <= 2)
{
return 1;
}
return Fibonacci(n - 1) + Fibonacci(n - 2);
}
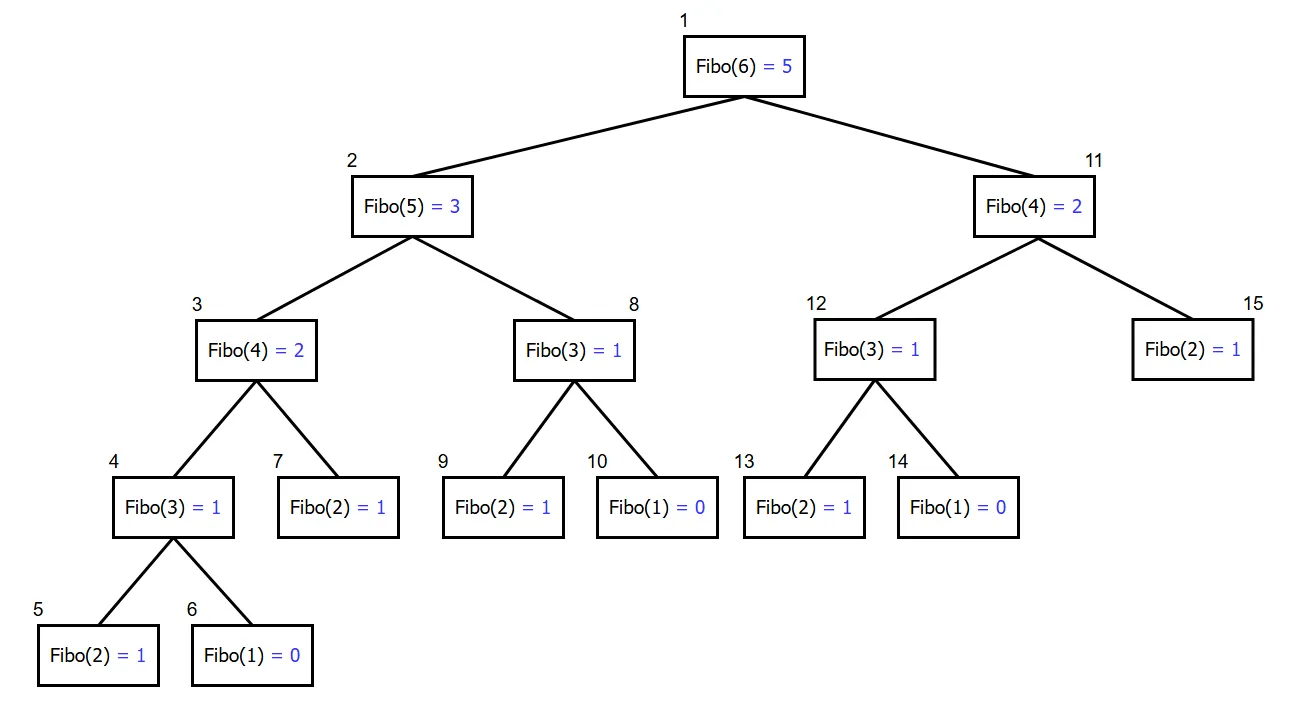
재귀호출 내에서 두 개의 Fibonacci 함수를 다시 재귀호출 하는데, +연산자 왼편에 있는 함수호출이 모두 완료되어야 비로소 +연산자 오른편에 있는 함수호출이 진행된다.
결국엔 Fibo$(n)$의 결과를 계산하기 위해서는 결국 $n = 1$혹은 $2$에 도달할 때까지 재귀 호출이 계속해서 이어진다. 그 과정에서 동일한 계산이 반복되므로 함수 호출 횟수가 기하급수적으로 늘어나게 된다.
3. 이진 탐색 알고리즘
이진 탐색은 정렬된 배열에서만 사용할 수 있는데, 이진탐색도 재귀호출로 구현할 수 있다.(물론 반복문이 더 효율적이다.)
탐색 과정은 다음과 같이 반복된다.
- 배열의 중간 원소와 찾는 값을 비교한다.
- 찾는 값이 더 작으면 탐색 범위를 first ~ mid - 1로 줄인다.
- 찾는 값이 더 크면 탐색 범위를 mid + 1 ~ last로 줄인다.
- 값이 일치할 때까지 위 과정을 반복한다.
public int BinarySearch(int[] arr, int first, int last, int target)
{
if (first > last) return -1;
var mid = (first + last) / 2;
// 찾아야 할 값이 중간값보다 작다면
if (arr[mid] > target)
{
return BinarySearch(arr, first, mid - 1, target);
}
// 찾아야 할 값이 중간값보다 크다면
else if (arr[mid] < target)
{
return BinarySearch(arr, mid + 1, last, target);
}
return mid;
}
재귀 함수에 익숙해지기 위해 이진 탐색을 재귀호출로 구현하였다. 이 외의 상황이라면, 반복문을 사용해서 구현하자.
■ 하노이 타워 : The Tower of Hanoi

하노이 타워도 재귀 호출의 대표적인 예시이다. 하노이 타워의 룰은 아래와 같다.
- 한 번의 하나의 원반만 옮길 수 있다.
- 옮기는 과정에서 작은 원반 위에 큰 원반이 올 수 없다.
- A 막대에 있는 원반을 모두 C막대로 옮긴다.

원반이 3개밖에 없기 때문에 조금만 고민하면 누구나 해결할 수 있다. 다만 원반의 수가 늘어나면 조금 복잡해지는데, 그래도 “일련의 과정”만 반복하면 해결할 수 있다.
- 여기서 말하는 “일련의 과정”이 바로 재귀이다.
우선 가장 큰 원반을 C로 가져다 놔야 한다. 그러기 위해선 가장 큰 원반을 제외한 원반들을 B 기둥으로 옮겨야 한다.
▶ 하노이 타워의 반복패턴

원반이 4개라면 가장 큰 원반을 제외하고 나머지 원반 3개를 B 막대로 이동해야 한다.

그 뒤, 가장 큰 원반을 C로 옮기고, B 막대에 남아있는 원반을 C로 옮기면 된다.
여기서 핵심은 원반 3개의 이동과정은 언급하지 않았는데, 이미 위에서 원반 3개를 이동하는 방법을 정리했기 때문이다.
그렇다면, 원반의 개수를 $n$으로 일반화하여 정리해 보자.
- 작은 원반 $n - 1$개를 A에서 B로 이동.
- 큰 원반 1개를 A에서 C로 이동.
- 작은 원반 $n-1$개를 B에서 C로 이동.
이렇게 원반 $n$개를 이동하는 문제는 원반 $n-1$개를 이동하는 문제로 세분화되고, 원반 $n-1$개를 이동하는 문제는 $n-2$개를 이동하는 문제로 세분화된다.
▶ 하노이 타워 문제 해결
public void HanoiTowerMove(int num, char from, char by, char to)
{
}
위 함수의 매개변수가 의미하는 바는, “num개의 원반을 from에서 by를 거쳐 to로 옮긴다”이다.
앞서 재귀호출을 작성할 때 무조건 “탈출 조건”부터 작성하라고 했는데, 하노이 타워에서의 탈출 조건은 이동해야 할 원반의 개수가 1인 경우이다.
public void HanoiTowerMove(int num, char from, char by, char to)
{
if(num <= 1)
{
Console.WriteLine($"원반 {num}을 {from}에서 {to}로 이동");
}
}
[탈출 조건 작성]
public void HanoiTowerMove(int num, char from, char by, char to)
{
if(num <= 1)
{
Console.WriteLine($"원반 {num}을 {from}에서 {to}로 이동");
}
else
{
// 원반 n개를 A->C로 옮기기 위해 n-1개를 먼저 b로 옮김
HanoiTowerMove(num - 1, from, to, by);
}
}
다음으로, 원반 $n$개를 C로 옮기기 위해 먼저 $n-1$개의 원반을 먼저 B로 옮겨야 한다. 이 역시 그대로 코드로 작성하면 위와 같다.
- 인자로 전달된 to가 by로 전달되고, by가 to로 전달된다. 이는 $n-1$개의 원반을 먼저 B로 옮기기 위함이다.
public void HanoiTowerMove(int num, char from, char by, char to)
{
if(num <= 1)
{
Console.WriteLine($"원반 {num}을 {from}에서 {to}로 이동");
}
else
{
// 원반 n개를 A->C로 옮기기 위해 n-1개를 먼저 b로 옮김
HanoiTowerMove(num - 1, from, to, by);
// 큰 원반을 A에서 C로 이동
Console.WriteLine($"원반 {num}을 {from}에서 {to}로 이동");
// 작은 원반 n-1개를 B->C로 이동
HanoiTowerMove(num - 1, by, from, to);
}
}

이제 나머지 과정을 그대로 추가해 주면 하노이 타워의 재귀 호출이 완료된다.
$n-1$개의 원반을 A→B로 옮겼으니, 남아있는 가장 큰 원반을 C로 옮기고, B에 있는 원반 $n-1$개를 C로 옮기면 된다.

직접 재귀 호출의 순서를 정리해 보면 더 명확히 이해할 수 있다.
하노이 타워의 재귀 호출의 경우, 1번 과정에서 $T(n-1)$번 이동, 2번에서 한번 이동, 3번 과정에서 $T(n-1)$번 이동하기 때문에,
$$ T(n) = 2T(n-1) + 1 $$
위와 같은 점화식을 세울 수 있고, 이 점화식을 풀면 원반의 개수가 n개일 때, 함수의 호출 횟수는 $T(n) = 2^n-1$이 된다.
- 따라서 원반의 갯수가 늘어날수록, 이동 횟수는 2배가 된다.
'Unity,C# > 자료구조' 카테고리의 다른 글
| [C#] 자료구조(Data Structure)와 시간복잡도 (4) | 2025.06.16 |
|---|---|
| [C#, Unity] 우선순위 큐(PriorityQueue) (0) | 2025.04.08 |
