■ 개요
Queue와 같이 FIFO(먼저 들어온 요소가 먼저 나감)처럼 삽입은 순서대로 하지만, 꺼낼 때는 우선순위가 높은(낮은) 순서로 꺼내지게 된다.
- 중복을 허용하며, 우선순위가 같다면 일반적으로 삽입 순서에 따라 처리되거나, 다른 기준으로 정렬될 수 있다.
■ Heap
우선순위 큐는 힙(Heap)을 사용해 구현하는데, 여기서 말하는 힙은 메모리 구조에서 말하는 힙이 아닌, “자료구조에서의 힙”을 의미한다.
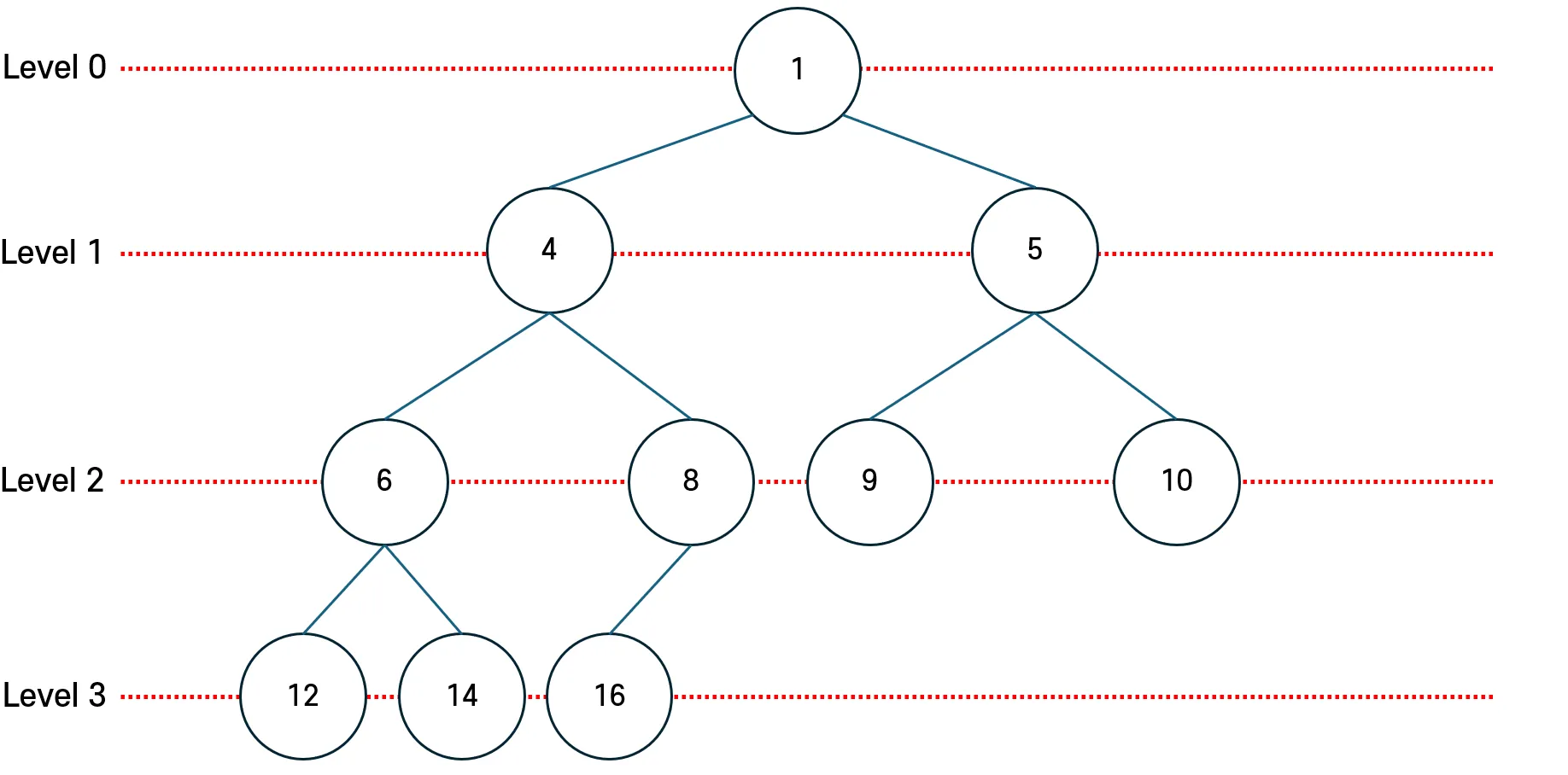
Heap 자료구조는 “완전 이진트리”로 구성된다.
- 모든 노드에 저장된 값은 자식 노드에 저장된 값보다 크거나(작거나) 같아야 한다.
- 마지막 레벨은 왼쪽부터 값이 채워진다.
- 위에서부터 내려갈수록 값이 커지면 Min-Heap, 값이 작아지면 Max-Heap이다.
- Min-Heap이던, Max-Heap이던 Root에 위치한 데이터가 가장 높은 우선순위를 가진다.
우선순위 큐에 저장되는 데이터는 모두 우선순위를 가져야 된다기보단, 데이터를 근거로 우선순위를 판단할 수 있어야 한다.
1. 데이터의 삽입(Min - Heap)

Heap에 데이터가 삽입될 때, 가장 마지막에 데이터를 먼저 삽입시킨다. 그 후 부모 노드와 우선순위를 비교한다.
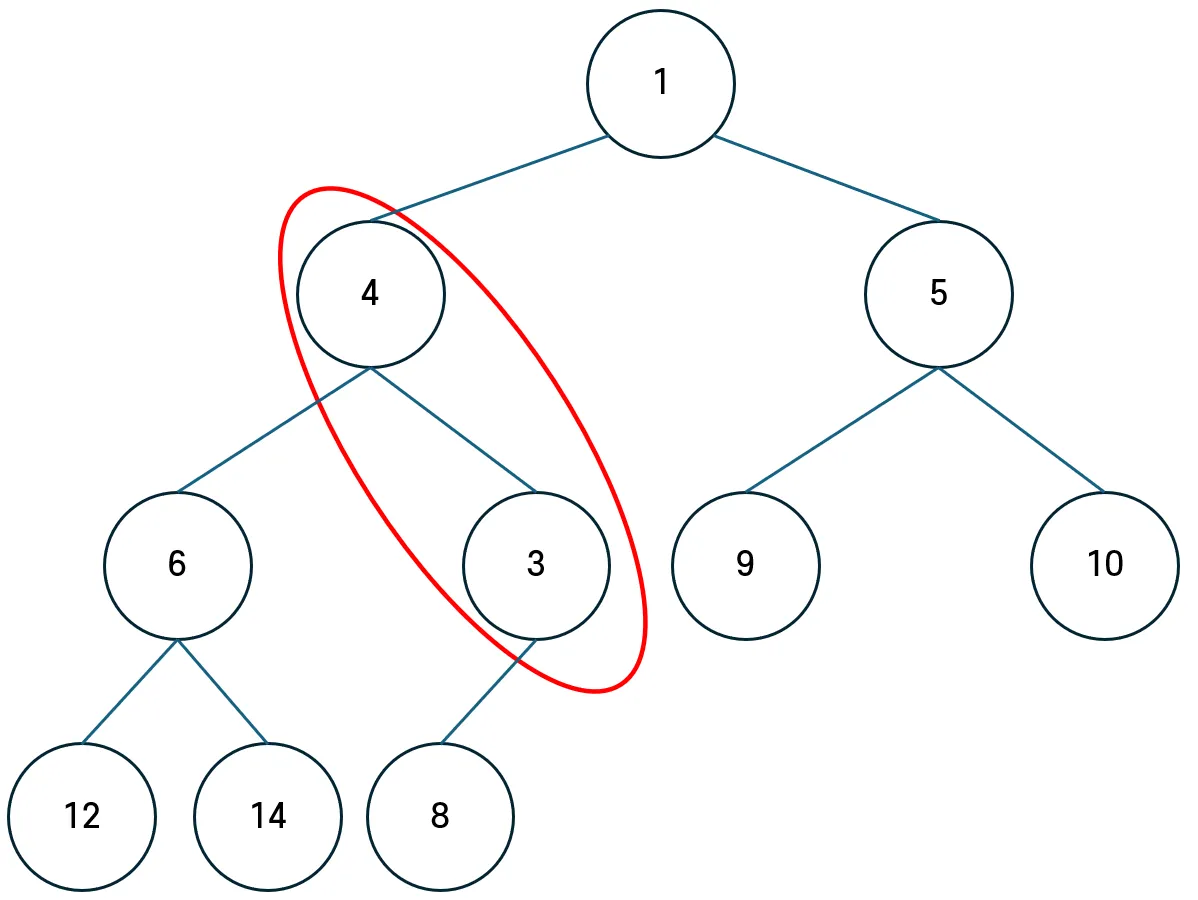
부모 노드의 우선순위가 더 높으므로, 부모 데이터와 자식 데이터를 교체한다. 이후 다시 한번 부모 노드와 우선순위를 비교한다.
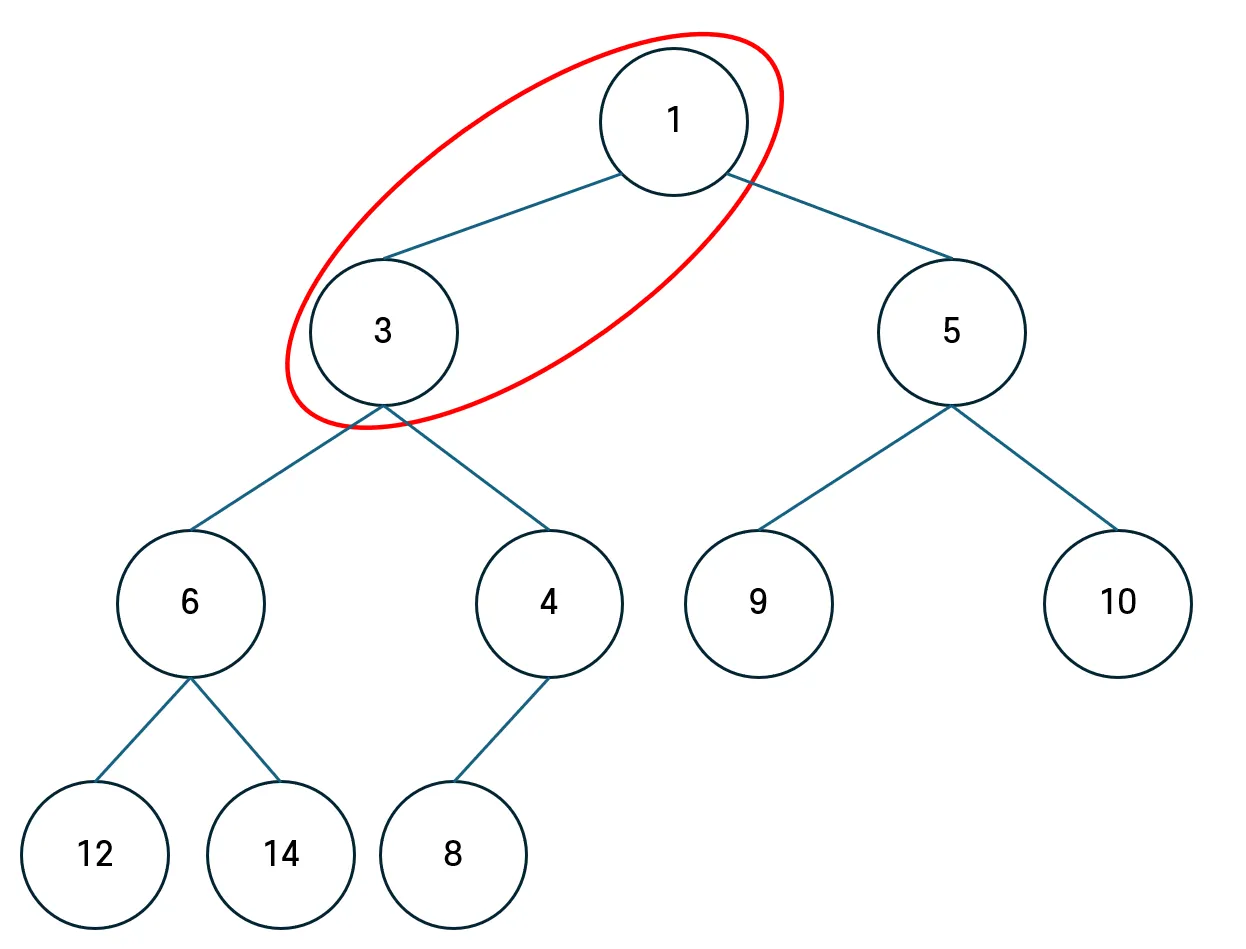
부모 노드의 우선 순위가 더 낮으므로 탐색을 종료한다.
▶ Min-Heap에서 우선순위가 9,10인 노드보다 8이 더 아래에 위치해 있는데요?
Heap자료구조는 “정렬된 트리”가 아니라 “구조와 조건”을 만족하는 트리이기 때문에 우선순위대로 정렬할 필요는 없다. 완전이진 트리의 조건을 다시 한번 정리하자면,
- 모든 레벨은 꽉 차있어야 한다.
- 따라서 제일 마지막에 원소가 채워진다.
- Min-Heap은 부모 <= 자식, Max-Heap 자식 <= 부모 이어야 한다.
위 조건만 만족하면 자식 노드들이 어떤 값을 가지고 있던, 좌우 순서나 깊이는 중요하지 않다.
2. 데이터의 삭제
우선순위 큐는 가장 우선순위가 높은 노드부터 삭제하기에, 무조건 루트 노드가 삭제된다.
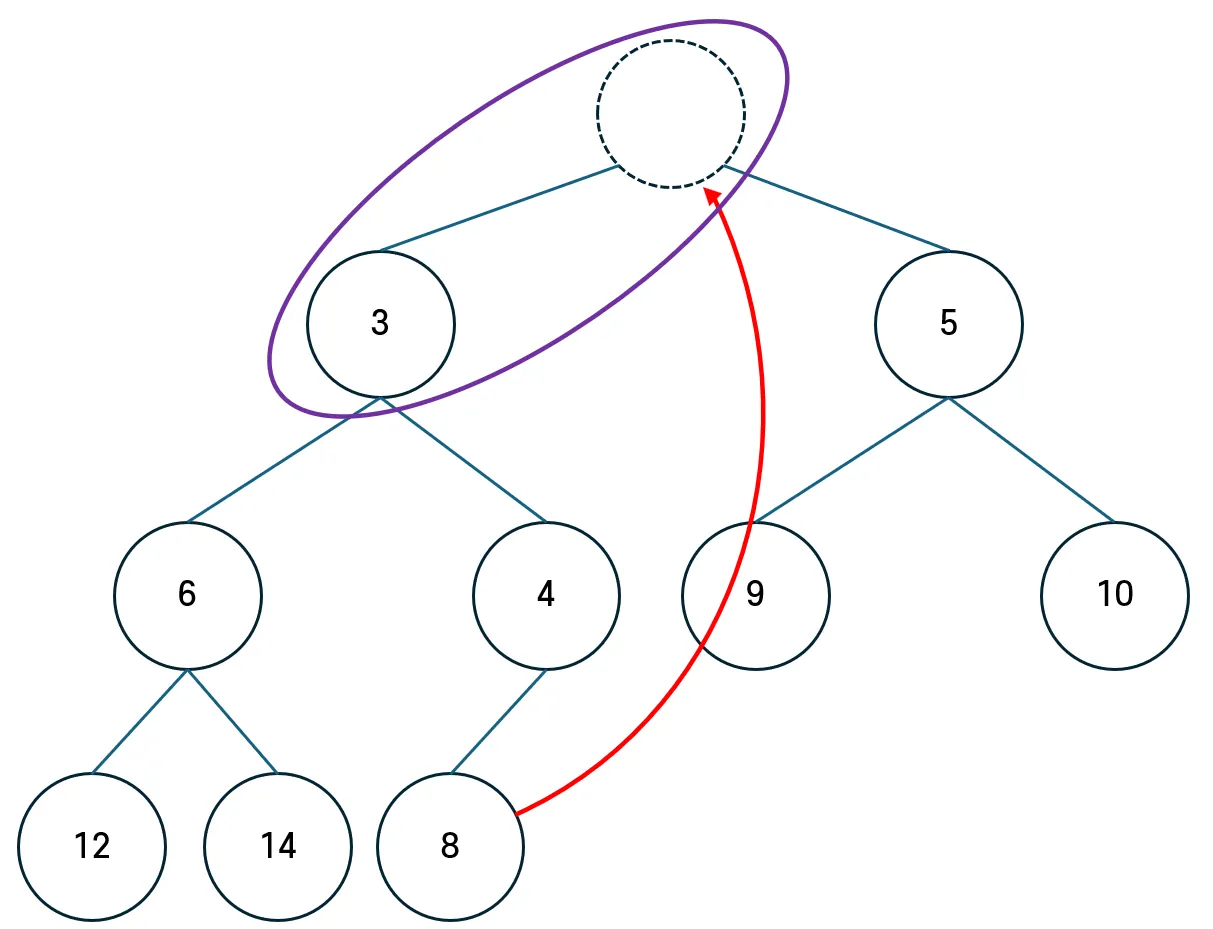
루트 노드가 삭제되면, 말단 노드를 루트 위치로 옮긴 뒤, 내려가면서 자식 노드와 비교를 진행한다.
- 이때, 무조건 왼쪽 노드의 자식부터 비교한다. (완전 이진트리는 왼쪽부터 채워지기 때문)
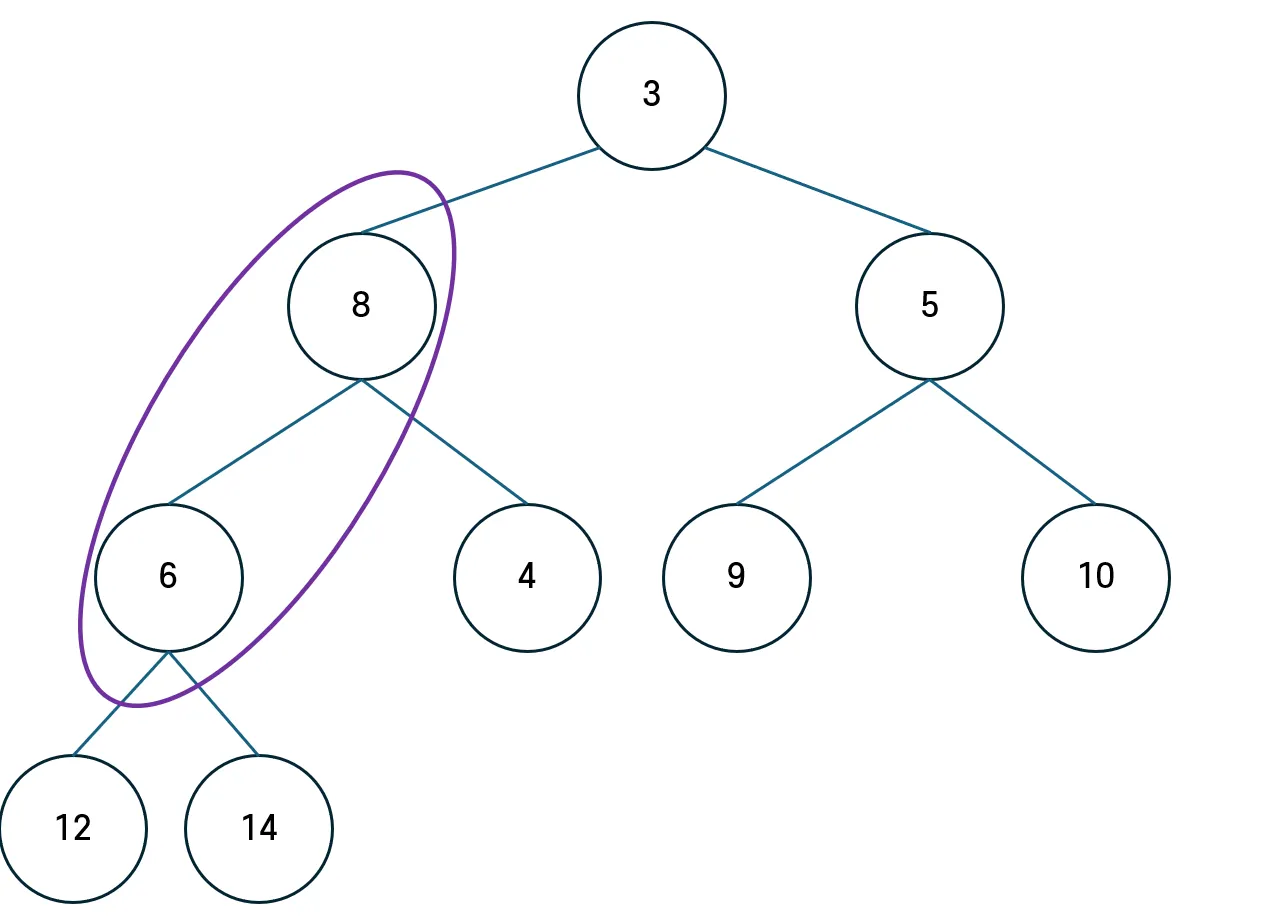
자식 노드 중 더 우선순위가 높은 쪽(= 값이 더 작은 쪽)과 비교해 Heap조건을 만족하지 않으면 교환하며 아래로 내려간다. 이 과정을 자식보다 값이 작거나 같아질 때까지 반복한다.
■ 우선순위 큐의 시간복잡도

우선순위 큐의 핵심 기능을 살펴보면 다음과 같다.
- Enqueue - 삽입
- Dequeue - 가장 우선순위 높은 요소 꺼내기
- Peek - 우선순위가 가장 높은 요소 확인
| 연산 | 시간복잡도 | 설명 |
| Enqueue | O(log n) | 가장 끝에 삽입 후, Heapify Up |
| Dequeue | O(\log n) | 루트를 제거하고, Heapify Down |
| Peek | O(1) | 루트를 바로 반환 |
Heap은 완전 이진트리 구조이기 때문에 트리의 높이만큼 비교/이동하면 되니까 시간복잡도는 O(log n)이 된다.
■ Unity(C#)에서 우선순위 큐 구현
유니티는. NET Standard 2.1을 사용하고, 우선순위 큐는. NET 6(C# 10)부터 도입된 클래스이기 때문에, 우선순위 큐는 사용이 불가능하다. 따라서 간단하게 우선순위 큐를 List로 구현해 보자.
using System;
using System.Collections.Generic;
public class PriorityQueue<TElement, TPriority> where TPriority : IComparable<TPriority>
{
private readonly List<(TElement element, TPriority priority)> _heap =
new List<(TElement, TPriority)>();
public int Count => _heap.Count;
}
List에는 <(TElement, TPriority)> 튜플이 저장된다. 여기서 TElement는 실제 저장할 데이터이고, TPriority는 이 데이터의 우선순위를 나타낸다.
- TPriority는 정렬을 위해 반드시 비교 가능한 타입이어야 하므로 IComparable<TPriority> 제약을 걸었다.
1. 부모/자식 인덱스

배열 기반의 완전 이진트리에서 부모/자식 인덱스를 찾는 공식은 다음과 같다.
| 관계 | 계산식 |
| 부모 → 왼쪽 자식 | left = n * 2 + 1 |
| 부모 → 오른쪽 자식 | Right = n * 2 + 2 |
| 자식 → 부모 | parent = (n - 1) / 2 |
- 우선순위 6번의 부모의 인덱스 = (3 - 1) / 2 = 1
- 우선순위 3번 노드의 왼쪽 자식과 오른쪽 자식의 인덱스
- 왼쪽 자식 = 1 * 2 + 1 = 3
- 오른쪽 자식 = 1 * 2 + 2 = 4
2. 요소 삽입 구현(Enqueue)
public bool Enqueue(TElement element, TPriority priority)
{
// 마지막 위치에 원소 추가
_heap.Add((element, priority));
var index = _heap.Count - 1;
while(index > 0)
{
// 부모 노드의 인덱스 구해오기
var parent = (index - 1) / 2;
// 현재 노드의 우선순위가 부모보다 크거나 같으면 (더 이상 위로 올릴 필요 없음)
if(_heap[index].priority.CompareTo(_heap[parent].priority) >= 0)
return true;
// 아니라면 부모와 자식을 스왑
(_heap[parent], _heap[index]) = (_heap[index], _heap[parent]);
index = parent;
}
}
요소를 맨 마지막에 추가시키고, 위로 올라가며 스왑 한다. 위에서 설명한 그대로 부모 노드의 인덱스를 얻어온 뒤 비교를 진행한다.
- 현재 노드의 우선순위가 부모 노드의 우선순위보다 크다면 종료하고, 아니라면 부모와 자식을 스왑한 뒤 인덱스를 갱신한다.
이건 Min-Heap 기준이고 Max-Heap이라면 조건을 반대로 두면 된다.
3. 요소 삭제 구현(Dequeue)
public bool TryDequeue(out TElement element, out TPriority priority)
{
if(_heap.Count <= 0)
{
element = default;
priority = default;
return false;
}
// 루트 요소 반환
element = _heap[0].element;
priority = _heap[0].priority;
// 마지막 요소를 루트에 위치시키고, 힙 크기를 줄임
var lastElement = _heap[^1];
_heap[0] = lastElement;
_heap.RemoveAt(_heap.Count - 1);
// 정렬 시작
var index = 0;
var count = _heap.Count;
while(true)
{
// 자식의 인덱스를 구함
var left = index * 2 + 1;
var right = index * 2 + 2;
var current = index;
// 좌측 자식의 우선순위가 현재 우선순위보다 낮다면
if(left < count && _heap[current].priority.CompareTo(_heap[left].priority) < 0)
{
current = left;
}
// 우측 자식의 우선순위가 현재 우선순위보다 낮다면
if(right < count && _heap[current].priority.CompareTo(_heap[right].priority) < 0)
{
current = right;
}
// 두 조건 다 만족하지 못한다면
if(current == index)
{
return true;
}
// 스왑 진행
(_heap[current], _heap[index]) = (_heap[index], _heap[current]);
index = current;
}
}루트 노드를 반환한 후, 가장 마지막에 있는 요소를 루트 위치로 올린다.
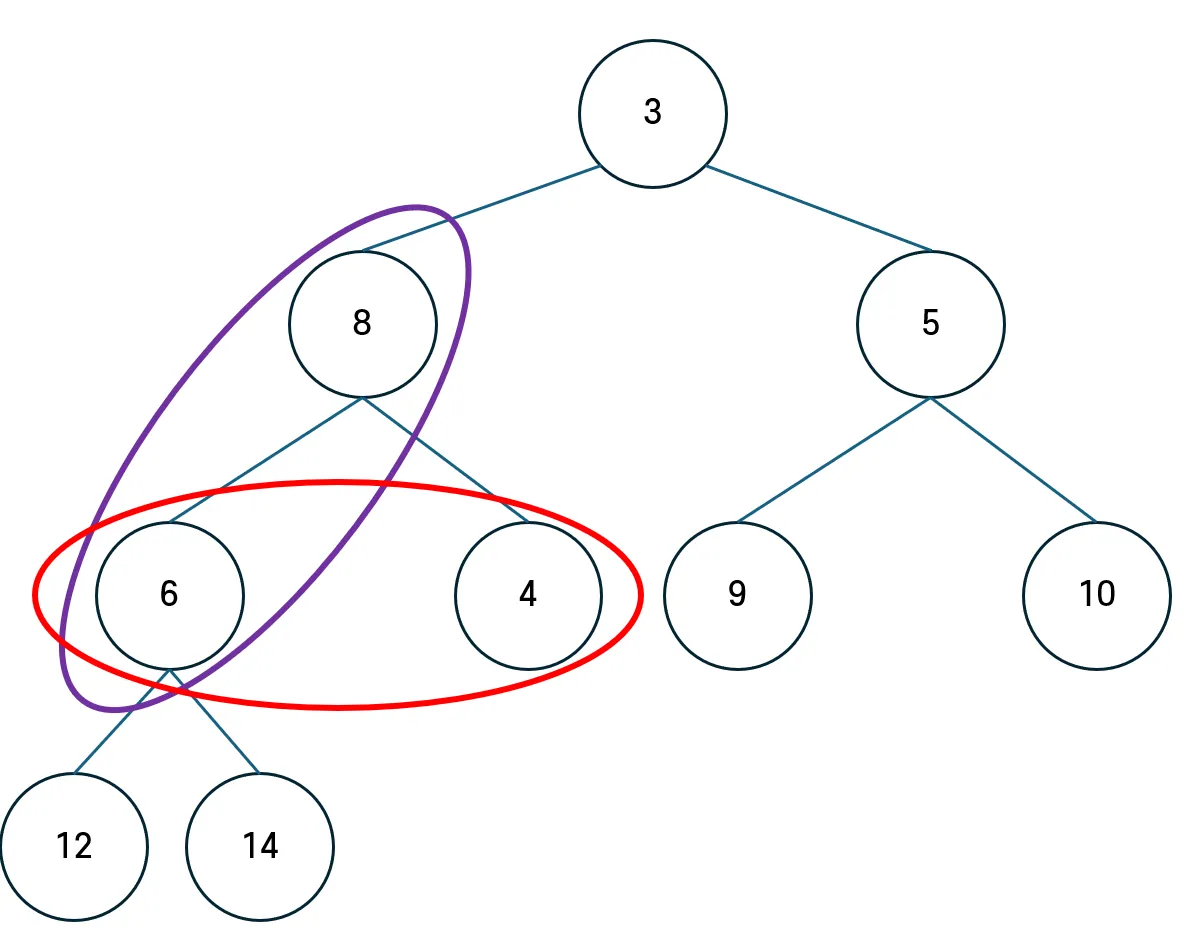
이후 Heap 조건(Min-Heap: 부모 ≤ 자식)을 유지하기 위해 자식 노드와 우선순위를 비교하며 아래로 내려가는 과정(Heapify Down)을 수행한다.
- 왼쪽과 오른쪽 자식 노드가 모두 존재할 경우, 둘 중 우선순위가 더 높은 노드(= 더 작은 우선순위 값)를 선택하여 비교한다.
- 예를 들어 왼쪽 자식의 우선순위가 6(인덱스 3)과 비교하면 current = 3이 되고, 이후 오른쪽 자식이 우선순위가 더 높으므로 current = 4로 갱신된다.
- 만약 현재 노드가 두 자식보다도 우선순위가 높다면(= 이미 최솟값이라면) Heap 조건을 만족하는 것이므로 정렬을 종료한다.
여기서 왼쪽과 오른쪽 두 자식과 모두 비교하여 더 “우선순위가 높은”자식과 스왑해야 하므로, 두 자식과 모두 비교해야 한다.
■ 전체 코드
using System;
using System.Collections.Generic;
public class PriorityQueue<TElement, TPriority> where TPriority : IComparable<TPriority>
{
private readonly List<(TElement element, TPriority priority)> _heap = new List<(TElement, TPriority)>();
public int Count => _heap.Count;
public bool Enqueue(TElement element, TPriority priority)
{
_heap.Add((element, priority));
var index = _heap.Count - 1;
while (index > 0)
{
var parent = (index - 1) / 2;
if (_heap[index].priority.CompareTo(_heap[parent].priority) >= 0)
return true;
(_heap[index], _heap[parent]) = (_heap[parent], _heap[index]);
index = parent;
}
return false;
}
public bool TryDequeue(out TElement element, out TPriority priority)
{
if (_heap.Count <= 0)
{
element = default;
priority = default;
return false;
}
element = _heap[0].Item1;
priority = _heap[0].Item2;
var lastElement = _heap[^1];
_heap[0] = lastElement;
_heap.RemoveAt(_heap.Count - 1);
var index = 0;
var count = _heap.Count;
while (true)
{
var left = 2 * index + 1;
var right = 2 * index + 2;
var current = index;
if (left < count && _heap[left].priority.CompareTo(_heap[current].priority) < 0)
{
current = left;
}
if (right < count && _heap[right].priority.CompareTo(_heap[current].priority) < 0)
{
current = right;
}
if (current == index)
{
return true;
}
(_heap[index], _heap[current]) = (_heap[current], _heap[index]);
index = current;
}
}
}
'Unity,C# > 자료구조' 카테고리의 다른 글
| [C#] 재귀호출(Recursive Call) / 팩토리얼, 피보나치, 하노이타워 (0) | 2025.10.03 |
|---|---|
| [C#] 자료구조(Data Structure)와 시간복잡도 (4) | 2025.06.16 |