■ 오일러 각의 단점
오일러 각은 적은 용량으로 3차원 공간의 회전 정보를 기록할 수 있고(행렬을 사용하면 최소 9개의 실수 데이터 필요), 사용자 입장에서 물체의 회전 각도를 쉽게 설정하는 데 사용된다.
하지만 오일러각에는 명확한 단점이 존재한다.
1. 짐벌락(Gimbal lock) 현상
짐벌락은 오일러 각을 사용할 때 세 번째 회전축이 첫 번째 회전축과 일치하게 되어 동일한 방향으로 회전하게 되는 현상이다.
이 짐벌락은 두 번째 축의 회전값이 $90^{\circ}$혹은 $-90^{\circ}(270^{\circ})$일 때 발생한다.
- 유니티는 오일러 각을 적용할 때 Z → X → Y 순서로 적용하여, X축이 90 혹은 -90일 때 짐벌락 현상이 발생한다.
유니티에서 짐벌락 현상을 재현하기 위해 오일러 각으로 물체를 회전시켜 보자.

x축을 기준으로 yz평면을 -90도 회전하면 비행기의 머리는 하늘을 바라보게 된다. 이제 이 상태에서 y, z 축 기준으로 yaw, roll 회전을 하면,


y축과 z축 회전(yaw, roll) 회전이 같아지게 된다. 이렇게 짐벌락 현상이 발생하는 이유는 오일러 각은 부모-자식 관계를 가지기 때문이다.
- Y(할아버지)
- X(아버지)
- Z(아들)
- X(아버지)
유니티에서 오일러 각은 위와 같은 계층 구조를 가지게 된다. 따라서 Y(할아버지)의 회전은 X, Z 축에 영향을 주고, X축의 회전은 Z 축에 영향을 주게 된다.
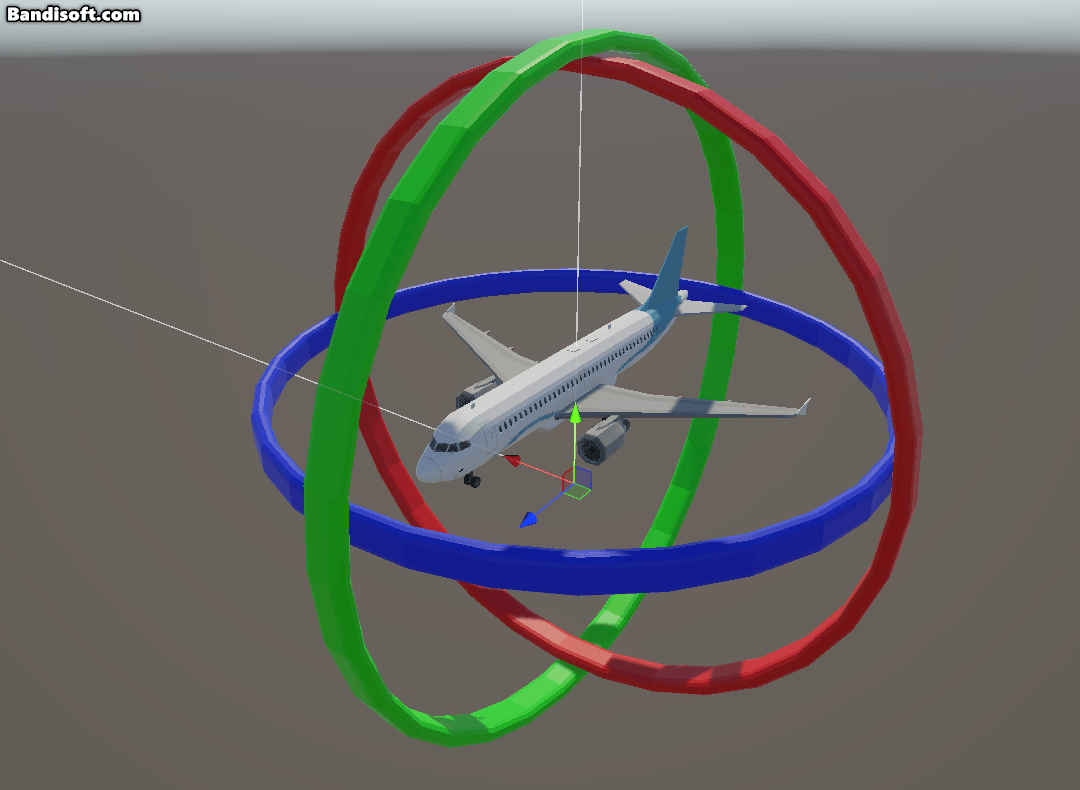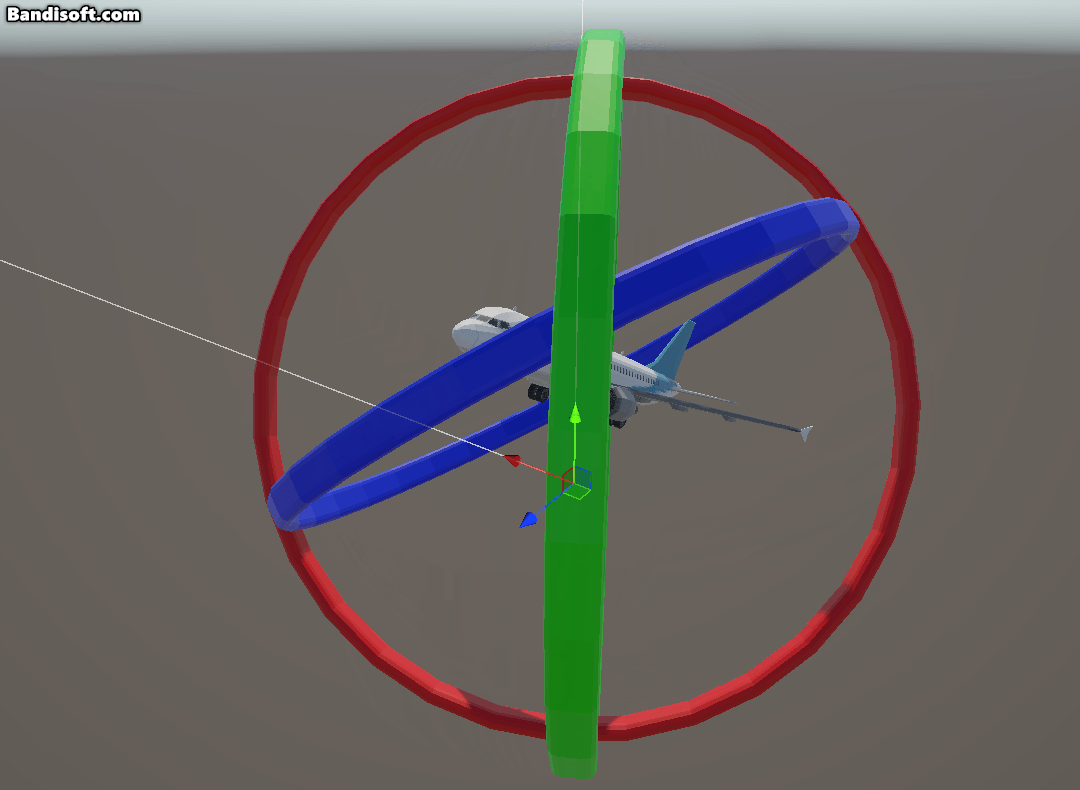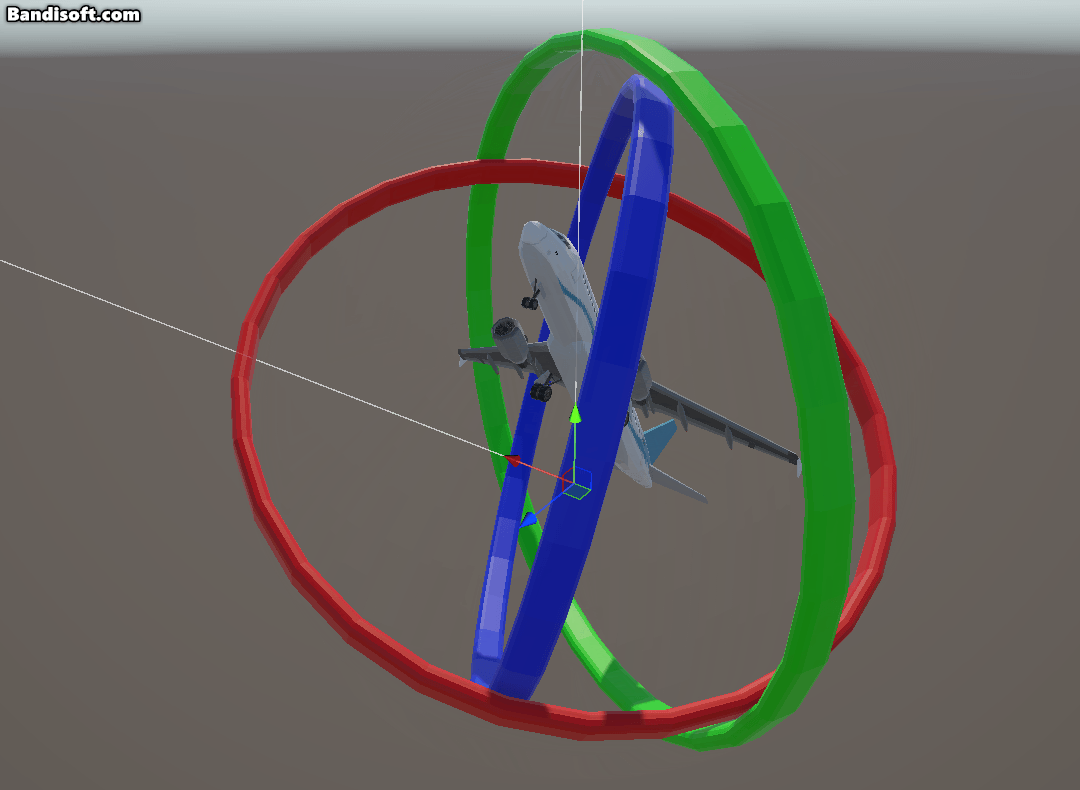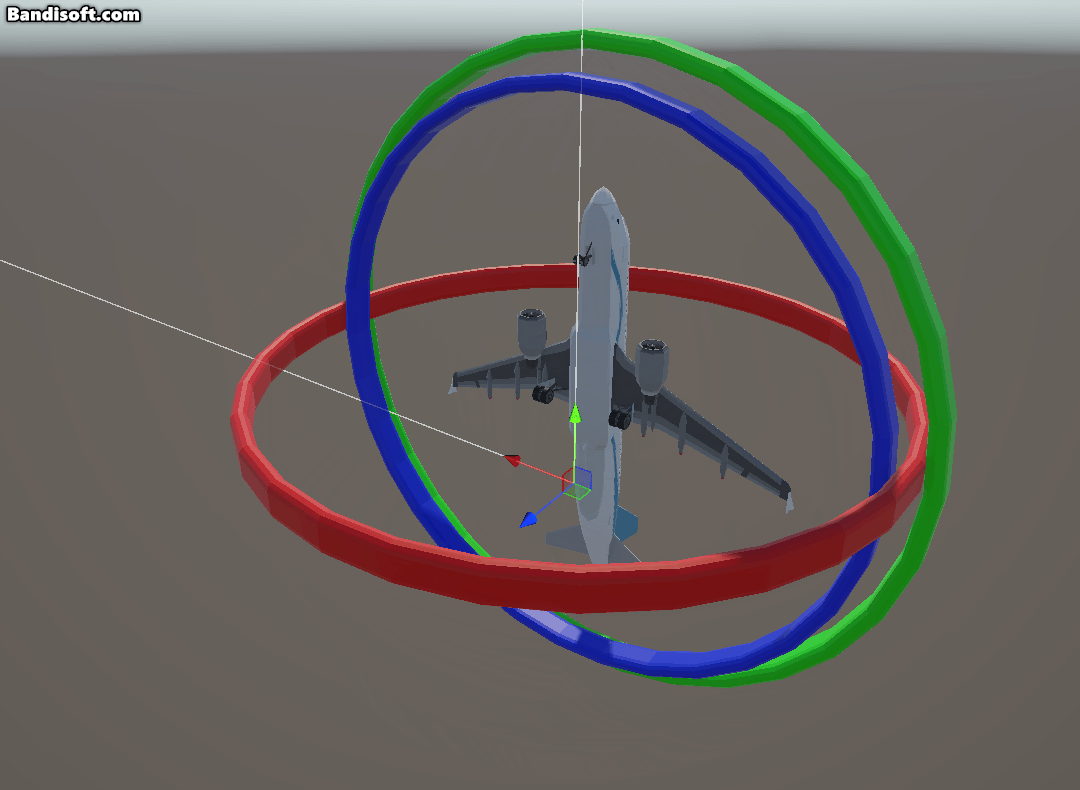
이때, 계층구조에서 중간축인 x축을 90도 회전하게 되면 Y와 Z가 같은 축으로 합쳐 “잠기게”된다. 이때 yaw와 roll이 구분되지 않고 동일한 효과가 되어 둘을 독립적으로 조절할 수 없게 된다.
🤔 회전행렬을 통한 짐벌락 현상 확인
짐벌락 현상을 회전행렬을 통해 알아보면 아래와 같다. 먼저, 유니티에서 오일러 각은 아래와 같이 계산된다.
$$ R_y \cdot R_x \cdot R_z = $$
\begin{bmatrix}\cos\alpha & 0 & \sin\alpha \\0 & 1 & 0 \\-\sin\alpha & 0 & \cos\alpha\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\0 & \cos\beta & -\sin\beta \\0 & \sin\beta & \cos\beta\end{bmatrix}\begin{bmatrix}\cos\gamma & -\sin\gamma & 0 \\\sin\gamma & \cos\gamma & 0 \\0 & 0 & 1\end{bmatrix}
[오일러 각 계산]
여기서 $R_x$를 90도 회전, 즉 $\beta = \pi /2$를 대입하면 $\cos \beta = 0$, $\sin\beta = 1$이 된다.
$$ R_y \cdot R_x \cdot R_z = $$
\begin{bmatrix}\cos\alpha & 0 & \sin\alpha \\0 & 1 & 0 \\-\sin\alpha & 0 & \cos\alpha\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\0 & 0 &- 1 \\0 & 1 & 0\end{bmatrix}\begin{bmatrix}\cos\gamma & -\sin\gamma & 0 \\\sin\gamma & \cos\gamma & 0 \\0 & 0 & 1\end{bmatrix}
[x축 90도 회전]
$$ R = R_y(\alpha)\,R_x(90^\circ)\,R_z(\gamma) = \begin{bmatrix}\cos(\alpha - \gamma) & \sin(\alpha - \gamma) & 0 \\[4pt]0 & 0 & -1 \\[4pt]-\sin(\alpha - \gamma) & \cos(\alpha - \gamma) & 0\end{bmatrix} $$
[최종 회전행렬]
$x = 90^{\circ}$일 때, $y$와 $z$가 $\alpha - \gamma$형태로 묶여버린다. 그래서 회전 자유도가 3→2로 줄어들고 Yaw와 Roll이 같은 축으로 작용하는 “짐벌락 상태”가 되어버린다.
🤔 Y축이 90도 회전한 경우
반대로 이번엔 $\alpha = \pi/2$ 즉, y축으로 90도 회전한 결과를 계산해 보자.
$$ R_y \cdot R_x \cdot R_z = \begin{bmatrix}0 & 0 & 1 \\0 & 1 & 0 \\-1 & 0 & 0\end{bmatrix}\begin{bmatrix}1 & 0 & 0 \\0 & \cos\beta & -\sin\beta \\0 & \sin\beta & \cos\beta\end{bmatrix}\begin{bmatrix}\cos\gamma & -\sin\gamma & 0 \\\sin\gamma & \cos\gamma & 0 \\0 & 0 & 1\end{bmatrix} $$
$$ R_y(90^\circ)\,R_x(\beta)\,R_z(\gamma)=\begin{bmatrix}\sin\beta\sin\gamma & \sin\beta\cos\gamma & \cos\beta \\[6pt]\cos\beta\sin\gamma & \cos\beta\cos\gamma & -\sin\beta \\[6pt]-\cos\gamma & \sin\gamma & 0\end{bmatrix} $$
[최종 회전행렬]
위의 경우 각 열(기저벡터)들이 여전히 서로 선형 독립인 상태이다. 따라서 $x = 90^{\circ}$일 때와 달리 두 축이 완전히 겹치지 않고, 짐벌락처럼 자유도도 사라지지 않았다.
행렬에서도 두 축의 항이 모두 남아있기 때문에 여전히 $\gamma$와 $\beta$가 서로 독립적으로 작용하고 있음을 확인할 수 있다.
2. 회전 보간
보간(Interpolation)은 두 값(또는 그 이상)의 알려진 값 사이에서 비율$(t)$에 따라 중간값을 계산하는 방법이다.
3차원 공간에서 두 회전(시작과 끝) 사이를 부드럽게 회전하기 위해 중간 회전 값을 계산해야 하는데, 이를 회전 보간(Rotation Interpolation)이라 한다.
$$ \theta' = (1-t)\theta_s + t\theta_e $$
[회전 보간식]
회전 보간이 3차원 공간의 오일러 각 회전에서 성립하는지 확인하려면 두 오일러 각의 회전 변환을 곱한 결과가 두 오일러 각의 합의 회전 변환과 동일한지 확인하면 된다.
- 회전 보간식이 올바르게 작동하라면 회전이 덧셈처럼 누적될 수 있어야 하고, 그 조건이 $R(a + b) = R(a) \cdot R(b)$이다.
🛠️ 한 축(Y)만 사용하는 경우
$y$축으로 $\alpha, \beta$만큼 회전한 오일러 각 데이터는 아래와 같다.
$$ (\alpha, 0,0) \\ (\beta, 0, 0) $$
또한, 위 오일러 각에 대응하는 회전 변환은 다음과 같이 계산할 수 있다.
$$ R_\alpha = R_{yaw\alpha} \cdot I\cdot I = R_{yaw\beta} \\ R_\beta= R_{yaw\beta} \cdot I\cdot I = R_{yaw\beta} $$
두 오일러 각을 합한 회전 변환은,
$$ R_{(\alpha + \beta)} = R_{yaw(\alpha+\beta)} \cdot I \cdot I = R_{yaw(\alpha+\beta)} $$
두 오일러 각에 대응되는 회전변환을 곱한 결과는,
$$ R_{\beta} \cdot R_{\alpha} = (R_{yaw\beta} \cdot I \cdot I) \cdot(R_{yaw\alpha} \cdot I \cdot I)\\ = R_{yaw\beta} \cdot R_{yaw\alpha} \\ =R_{yaw(\beta + \alpha)} $$
y축만 사용한 두 오일러 각을 곱한 결과는, 두 오일러 각을 합한 회전 변환과 동일함을 확인할 수 있다.
오일러 각에서 한 축만 사용한다는 것은, 2차원 평면에서의 회전과 동일하기 때문에 회전 보간식을 사용하는데 아무런 문제가 없다.
🛠️ 두 개의 축(x, y)만 사용하는 경우
그렇다면 두 축에 대해서도 회전 보간을 동일하게 사용할 수 있는지 확인해 보자. 두 축에 대해 회전하는 오일러 각의 데이터는 아래와 같다.
$$ (\alpha, \alpha, 0) \\ (\beta, \beta, 0) $$
두 각에 대응되는 회전 변환은 아래와 같이 계산된다.
$$ R_{\alpha} = R_{\text{yaw}\alpha} \cdot R_{\text{pitch}\alpha} \cdot I = R_{\text{yaw}\alpha} \cdot R_{\text{pitch}\alpha} \\ R_{\beta} = R_{\text{yaw}\beta} \cdot R_{\text{pitch}\beta} \cdot I = R_{\text{yaw}\beta} \cdot R_{\text{pitch}\beta} $$
두 오일러 각을 합한 회전 변환$(R_{(\alpha + \beta)})$은,
$$ R_{(\alpha + \beta)} = R_{\text{yaw}(\alpha + \beta)} \cdot R_{\text{pitch}(\alpha + \beta)} \cdot I = R_{\text{yaw}(\alpha + \beta)} \cdot R_{\text{pitch}(\alpha + \beta)} $$
두 오일러 각에 대응하는 회전 변환을 곱한 결과는,
$$ R_{\beta} \cdot R_{\alpha} = \left( R_{\text{yaw}\beta} \cdot R_{\text{pitch}\beta} \cdot R_{\text{roll}\beta} \right) \cdot \left( R_{\text{yaw}\alpha} \cdot R_{\text{pitch}\alpha} \cdot R_{\text{roll}\alpha} \right) \\ = \left( R_{\text{yaw}\beta} \cdot R_{\text{pitch}\beta} \cdot I \right) \cdot \left( R_{\text{yaw}\alpha} \cdot R_{\text{pitch}\alpha} \cdot I \right) \\ = R_{\text{yaw}\beta} \cdot R_{\text{pitch}\beta} \cdot R_{\text{yaw}\alpha} \cdot R_{\text{pitch}\alpha} \\ \neq R_{(\alpha + \beta)} $$
두 오일러 각에 대응되는 회전 변환을 곱한 결과는 두 오일러 각을 합한 회전 변환과 다르다. 따라서 두 축 이상을 사용하는 오일러 각은 선형 보간식을 사용할 수 없다.
- 3차원 공간에서 자유로운 회전 보간을 사용하기 위해선, 로드리게스 회전 공식 혹은 사원수를 사용해야 한다.
'게임수학' 카테고리의 다른 글
| [게임수학] 9-2. 외적(2) - 카메라의 회전 행렬, 로드리게스 공식 (0) | 2025.11.11 |
|---|---|
| [게임수학] 9-1. 외적(Cross product) (0) | 2025.11.11 |
| [게임수학] 8-1. 오일러 각(Euler's angle) (0) | 2025.10.14 |
| [게임수학] 7. 게임 엔진 (0) | 2025.09.24 |
| [게임수학] 6.삼각형(Mesh) (0) | 2025.09.20 |