→ 이 글은 「이득우의 게임 수학」을 바탕으로 작성했습니다.
■ 벡터로부터 회전행렬 생성
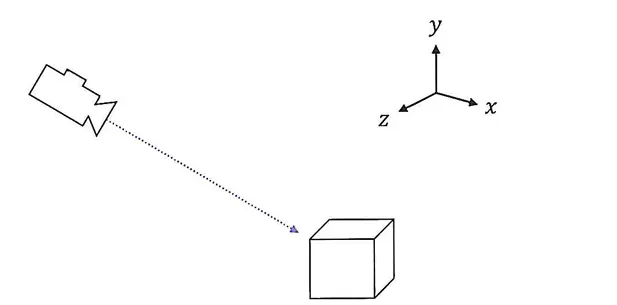
위와 같이 3차원 공간에서 좌우로 기울어지지 않는 카메라가 아래에 위치한 물체를 바라보고 있는 상황을 설정해 보자.
앞서 다룬 오일러 각 방식을 사용해 카메라의 회전을 지정할 수 있지만, 외적을 사용하면 카메라의 시선 벡터로부터 3개의 로컬 축을 구하고 이를 통해 회전 행렬을 얻어낼 수 있다.
1. 카메라의 로컬 z 축 계산
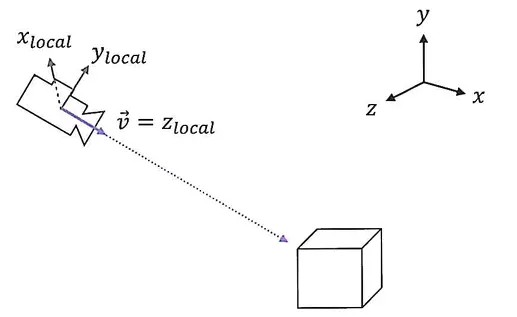
물체의 위치에서 카메라의 위치를 뺀 후 크기를 1로 정규화시킨 벡터$\vec v$를 생성하면, 이 벡터는 카메라 트랜스폼의 로컬 $z$축이 된다.
2. 카메라의 로컬 x, y 축 계산

월드 공간의 $y$축 벡터를 $\vec u$로 표시하고, 앞서 구한 로컬 $z$축과 외적 한 후 정규화시키면 카메라의 로컬 $x$축이 구해진다.
- 외적은 두 벡터에 수직인 벡터를 만들어낸다.

마찬가지로 앞서 구한 로컬 $z$축과 $x$축을 외적 하면 마지막으로 남은 로컬 $y$축을 구할 수 있다.
정리하자면, 카메라의 시선 벡터와 주어지는 업벡터$(\vec u)$로부터 카메라의 세 로컬 축은 아래와 같이 구할 수 있다.
$$ \vec x = \frac{\vec u \times \vec z}{|\vec u \times \vec z|}\\ \vec y = \vec z \times \vec x\\ \vec z = \frac{\vec v}{|\vec v|} $$
카메라 트랜스폼의 회전행렬$R$은 로컬 벡터를 열벡터로 지정해 아래와 같이 생성할 수 있다.
$$ R =\begin{bmatrix}x_x & y_x & z_x & 0 \\x_y & y_y & z_y & 0 \\x_z & y_z & z_z & 0 \\0 & 0 & 0 & 1\end{bmatrix} $$
[카메라의 회전행렬]
3. 예외 사항

위와 같이 카메라가 뒤집힌 경우라면, 기존 월드의 $y$축과 반대 방향인 벡터$\vec u$를 사용해 외적해야 한다.
- 따라서 외적에 사용될 업벡터의 값을 입력받도록 설계하는 것이 안전하다.

로컬 $z$축과 월드의 $y$축이 평행하면 외적 결과가 영벡터가 되어 더 이상 계산을 진행할 수 없다.
- 이러한 경우 외적 대신 로컬 $z$축에 직교하는 로컬 $x$축의 값을 수동으로 지정해줘야 한다.
■ 로드리게스 회전 공식
앞서 배웠던 오일러 각은 짐벌락이 발생하고 회전 보간 계산이 어렵다는 문제가 있었다.
이러한 오일러 각의 문제를 “임의의 축에 대한 평면의 회전 방식”을 사용하여 해결한 것이 바로 축-각 회전(Axis-Angle rotation)이다.
- 축-각 회전을 수행하는 회전 공식을 내적과 외적을 사용해 유도해 보자.
1. 회전 평면의 설정

회전축은 회전이 발생하는 평면에 직교하는 법선 벡터$(\vec n)$이다. 계산하기 편하기 이를 정규화시키고 각 기호의 의미는 아래와 같다.
- $O$ : 월드 공간의 원점.
- $O'$ : 회전 평면의 중심점.
- $P :$ 회전시킬 점.
- $P' :$ 점 $P$가 각 $\theta$만큼 회전한 최종 점.
이때 점 $P$의 좌표는 $P = (x,y,z,1)$로 설정한다. 그러고 나서 원점 $O$에서부터 회전시킬 점 $P$까지의 벡터를 $\vec u$로 지정하자.
- 점 $P$와 벡터 $\vec u$의 값은 마지막 차원의 값만 다를 뿐 $(x,y,z)$의 값은 동일하다.
$$ \vec u = P - O = (x,y,z,0) $$
2. 벡터 u를 정규화된 법선 벡터 n에 투영

원점에서 점 $P$로 항하는 벡터$\vec u$를 법선 단위벡터 $\hat n$에 투영하자. 법선 벡터의 크기가 1이므로, 투영 벡터 $\vec v$는 아래와 같이 계산된다.
$$ \vec{OO'} = \vec v = (\vec u \cdot \hat n) \cdot \hat n $$
그러면, 회전 평면의 중심점 $O'$에서 점 $P$로 향하는 벡터는 $\hat n$에 대한 $\vec u$의 수직 성분이므로, 투영 벡터를 빼면 다음과 같이 수직 성분을 구할 수 있다.
$$ \vec{O'P} = \vec u - \vec v $$
3. 회전 평면에서의 회전
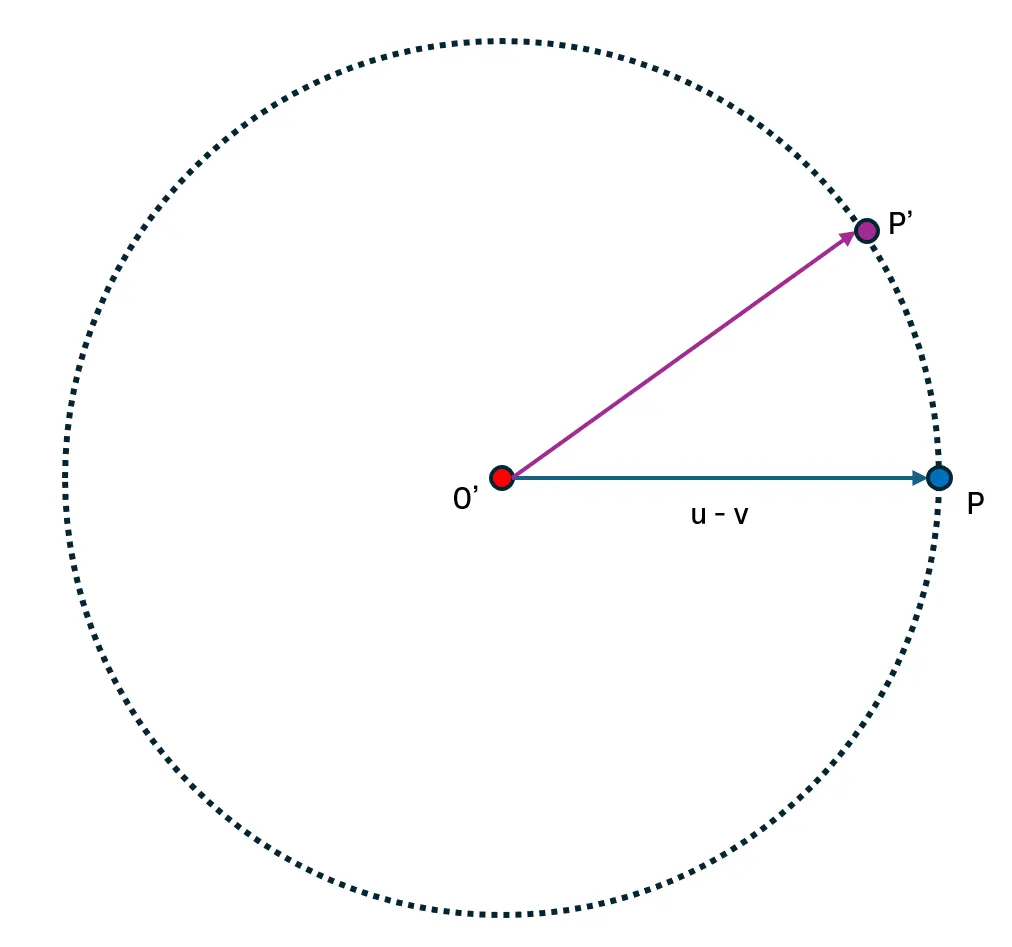
회전 평면을 위에서 내려다보면 위와 같은 모습이 되고, 최종적으로 회전이 끝난 벡터 $\vec {O'P'}$을 구하는 것이 목표이다.
이를 구하기 위해 벡터 $\vec {O'P'}$를 가로 성분과 세로 성분으로 분리해 보자.

$\vec {O'P'}$ 을 $\vec{O'P}$에 투영하면 가로 성분을 얻을 수 있으며, 이는 $\cos\theta(\vec u - \vec v)$로 표현할 수 있다.
남은 세로 성분은 법선 벡터 $\hat n$과 $\vec {O'P}$을 외적하면 얻을 수 있다. 이를 $\vec {O'Q}$로 지정하면, 아래와 같이 구할 수 있다.
$$ \vec {O'Q} = \hat n \times(\vec u - \vec v) $$
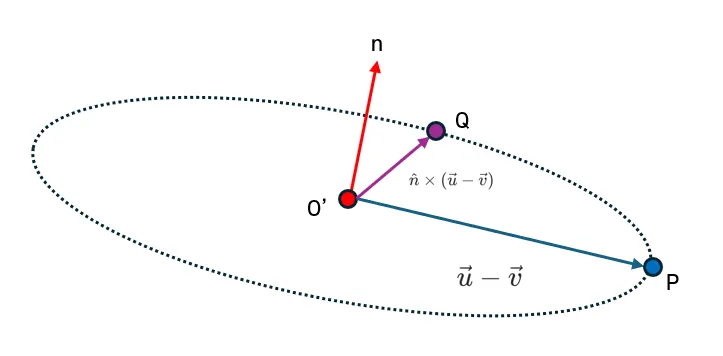
평면 위의 가로 성분을 $\cos\theta$만큼 유지하고, 세로 방향 성분에 $\sin\theta$비율로 추가하여 각도 $\theta$만큼 회전한 벡터를 만든다. 따라서 회전한 벡터 $\vec {O'P'}$는 다음과 같이 구할 수 있다.
$$ \vec {O'P'} = \cos\theta \cdot \vec{O'P} + \sin\theta \cdot \vec{O'Q} $$
위 식을 벡터를 사용해 전개하면,
$$ \vec{O'P'} = \cos\theta \cdot(\vec u - \vec v) + \sin\theta\cdot(\hat n\times(\vec u - \vec v)) $$
분배 법칙을 적용하면,
$$ \vec{O'P'} = \cos\theta \cdot(\vec u - \vec v) + \sin\theta\cdot(\hat n\times\vec u - \hat n \times \vec v) $$
벡터 $\hat n$과 $\vec v$는 평행하므로 우변의 끝에 위치한 $\hat n \times \vec v$의 결과는 항상 영벡터가 된다. 따라서 이 식은 다음과 같이 정리된다.
$$ \vec{O'P'} = \cos\theta \cdot(\vec u - \vec v) + \sin\theta\cdot(\hat n\times\vec u) $$
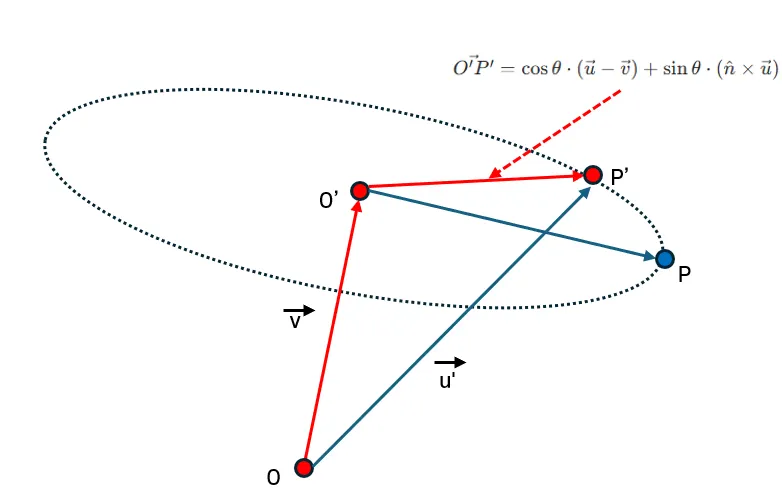
우리가 구할 최종 벡터 $\vec {OP'}$는 위와 같이 $\vec {O'P'}$에 $\vec v$를 더해 구할 수 있다. $\vec v = (\vec u\cdot \hat n)\cdot \hat n$이므로, 최종적으로 식은 다음과 같이 유도된다.

위 공식은 1840년에 프랑스 수학자 로드리게스(Olinde Rodrigues)가 발표했으며, 그의 이름을 인용해 로드리게스 회전 공식이라고 한다.
다만, 이 방식은 행렬로의 변환이 어려워 로드리게스 회전과 동일한 기능을 제공하면서도 간결하고 행렬로 변환도 용이한 사원수를 사용한다.
■ 로드리게스 - 유니티에서 구현
$$ \vec u' = \cos\theta\vec u + (1-\cos\theta)(\vec u\cdot\hat n)\cdot \hat n + \sin\theta(\hat n\times\vec u) $$
앞서 수식을 정리했으니 유니티에서 구현도 크게 어려운 것이 없다. 로드리게스 공식이 제대로 작동하는지 수식을 그대로 코드로 옮겨 확인해 보자.
using System;
using UnityEngine;
public class RodriguesRotation : MonoBehaviour
{
[SerializeField] private Transform axis;
[SerializeField] private float angle = 0f;
private void Update()
{
var axisNormal = axis.up;
var originToObj = transform.position - axis.position;
var t = angle * Mathf.Deg2Rad;
var ct = Mathf.Cos(t);
var st = Mathf.Sin(t);
var rotated = originToObj * ct +
axisNormal * Vector3.Dot(axisNormal, originToObj) * (1f - ct) +
Vector3.Cross(axisNormal, originToObj) * st;
transform.position = axis.position + rotated;
}
}
- axisNormal = $\hat n$ : 축이 되는 물체의 법선 벡터
- originToObj = $\vec u$ : 회전 중심점(축) → 회전 대상 물체 벡터
- t = $\theta$ : 회전시킬 각도.
위와 같이 변수들을 설정하면, 축 오브젝트(axis)를 기준으로 물체가 일정한 각도만큼 회전하는 것을 알 수 있다.
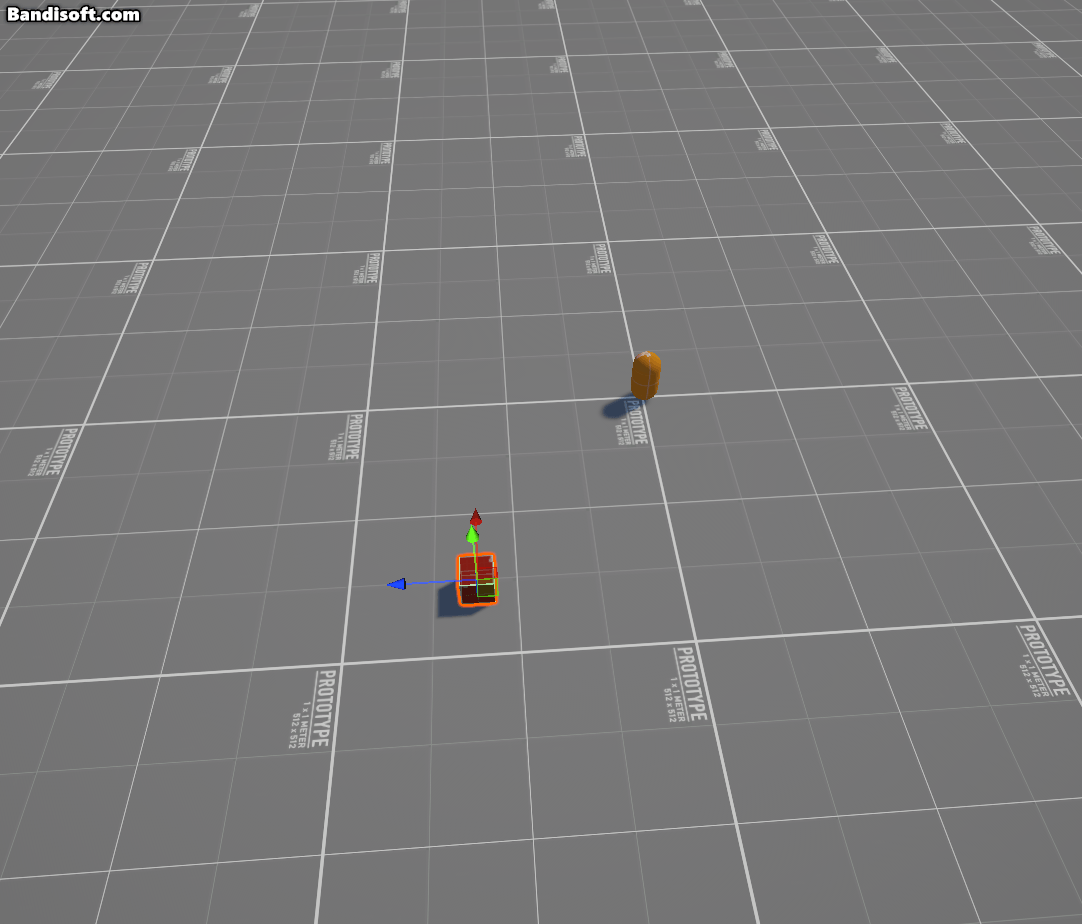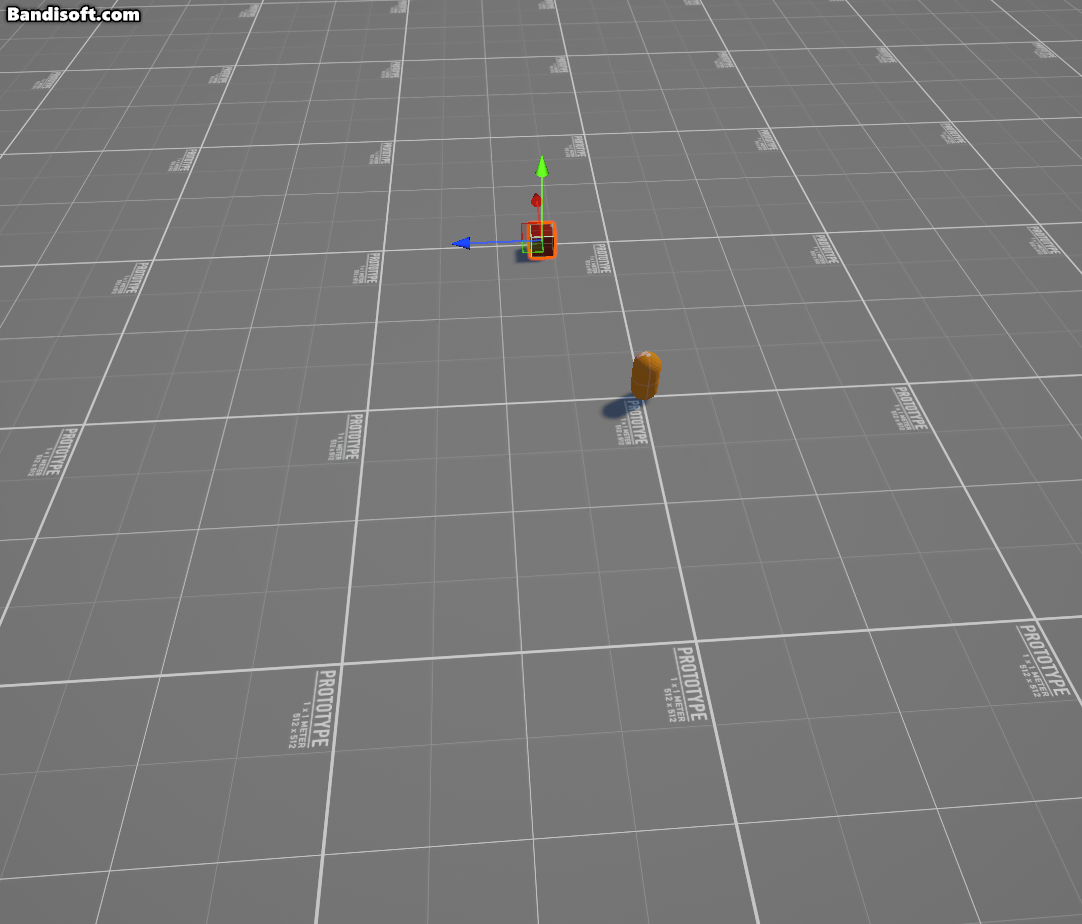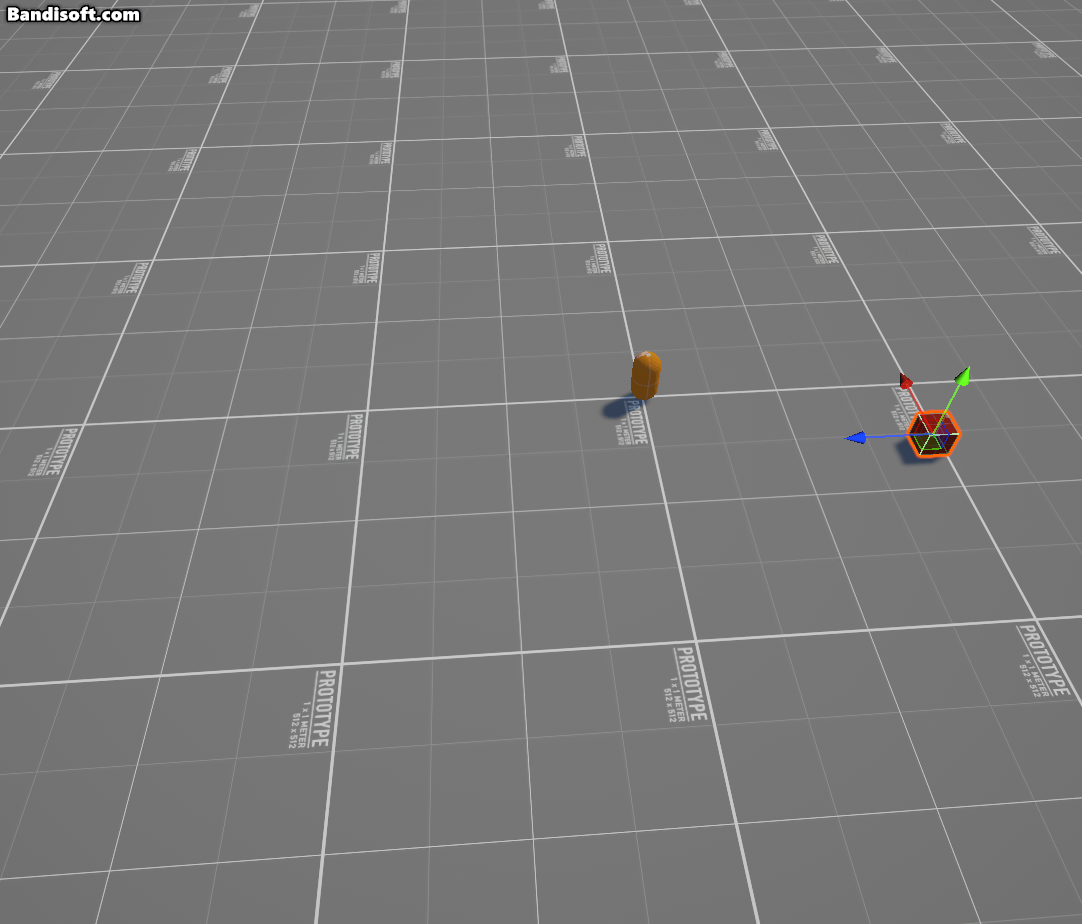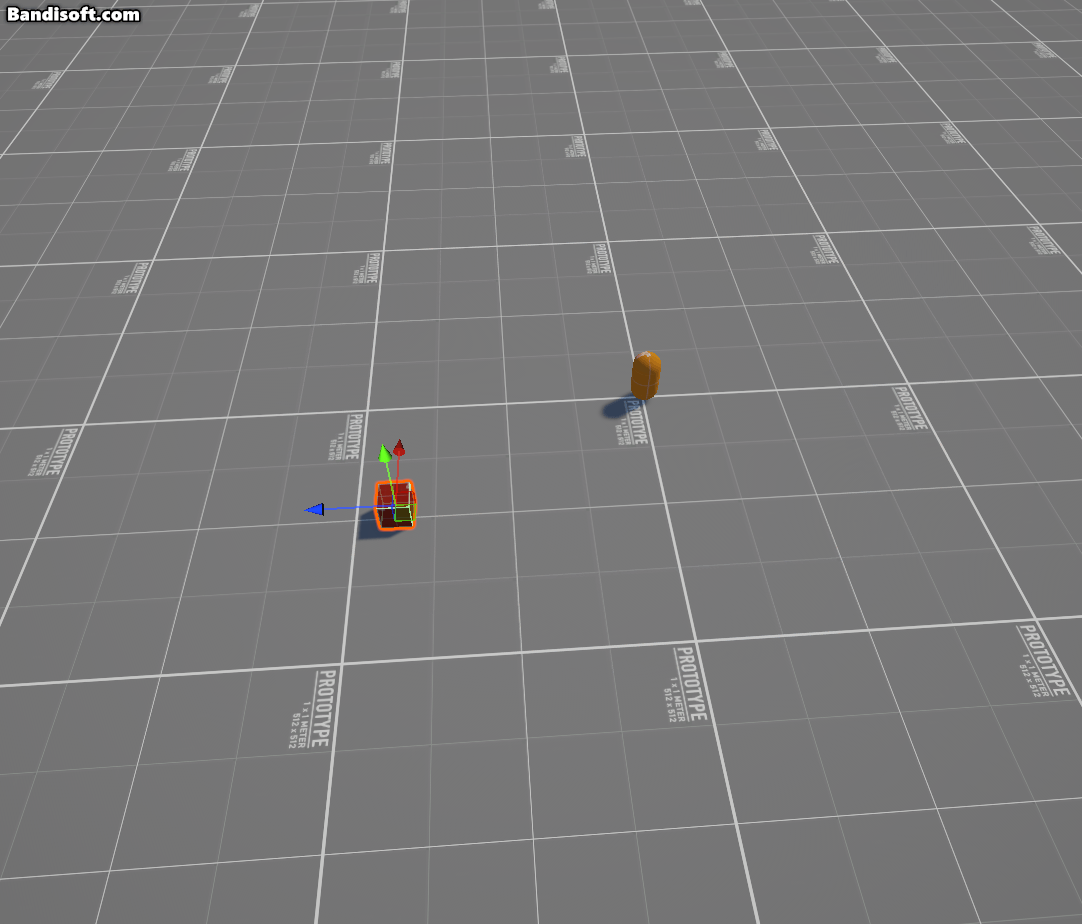
뭐 당연하겠지만, Unity에는 로드리게스 공식을 그대로 구현한 것과 동일한 기능을 하는 내장 함수 두 개가 이미 존재한다.
1. Quaternion.AngleAxis()
private void Update()
{
// Quaternion.AngleAxis() 사용
var axisToObj = transform.position - axis.position;
var rotated = Quaternion.AngleAxis(angle, axis.up) * axisToObj;
transform.position = axis.position + rotated;
}
[Quaternion.AngleAxis()]
Quaternion.AngleAxis()는 축을 기준으로 $\theta$만큼 회전하는 회전행렬을 사원수 형태(Quaternion)로 반환한다.
즉, 회전의 값 자체를 정의하는 함수이다.
- 주로 자기 자신의 축을 기준으로 회전(자전) 할 때 사용한다.
2. transform.RotateAround()
// transform.RotateAround(Vector3 point, Vector3 axis, float angle)
transform.RotateAround(axis.position, axis.up, angle);
[transform.RotateAround()]
이 함수는 특정 점(point)을 기준으로 오브젝트를 회전시킨다. 즉, 로드리게스 식과 완전히 동일한 동작을 수행한다.
- 자신이 아닌 다른 점을 기준으로 회전(공전, 궤도 회전)할 때 사용한다.
'게임수학' 카테고리의 다른 글
| [게임수학] 9-3. 외적(3) - 삼중곱 (0) | 2025.11.11 |
|---|---|
| [게임수학] 9-1. 외적(Cross product) (0) | 2025.11.11 |
| [게임수학] 8-2. 오일러 각의 단점(짐벌락, 회전 보간) (0) | 2025.10.14 |
| [게임수학] 8-1. 오일러 각(Euler's angle) (0) | 2025.10.14 |
| [게임수학] 7. 게임 엔진 (0) | 2025.09.24 |